The game can be borrowed from the IFEN's Centre of Pedagogical Documentation or the F.use (Future Spaces for Education) on the Belval Campus.
Involution
1#Involution

1.2 Lesson planning
01
Theme of the lesson in the overall structure of the axes
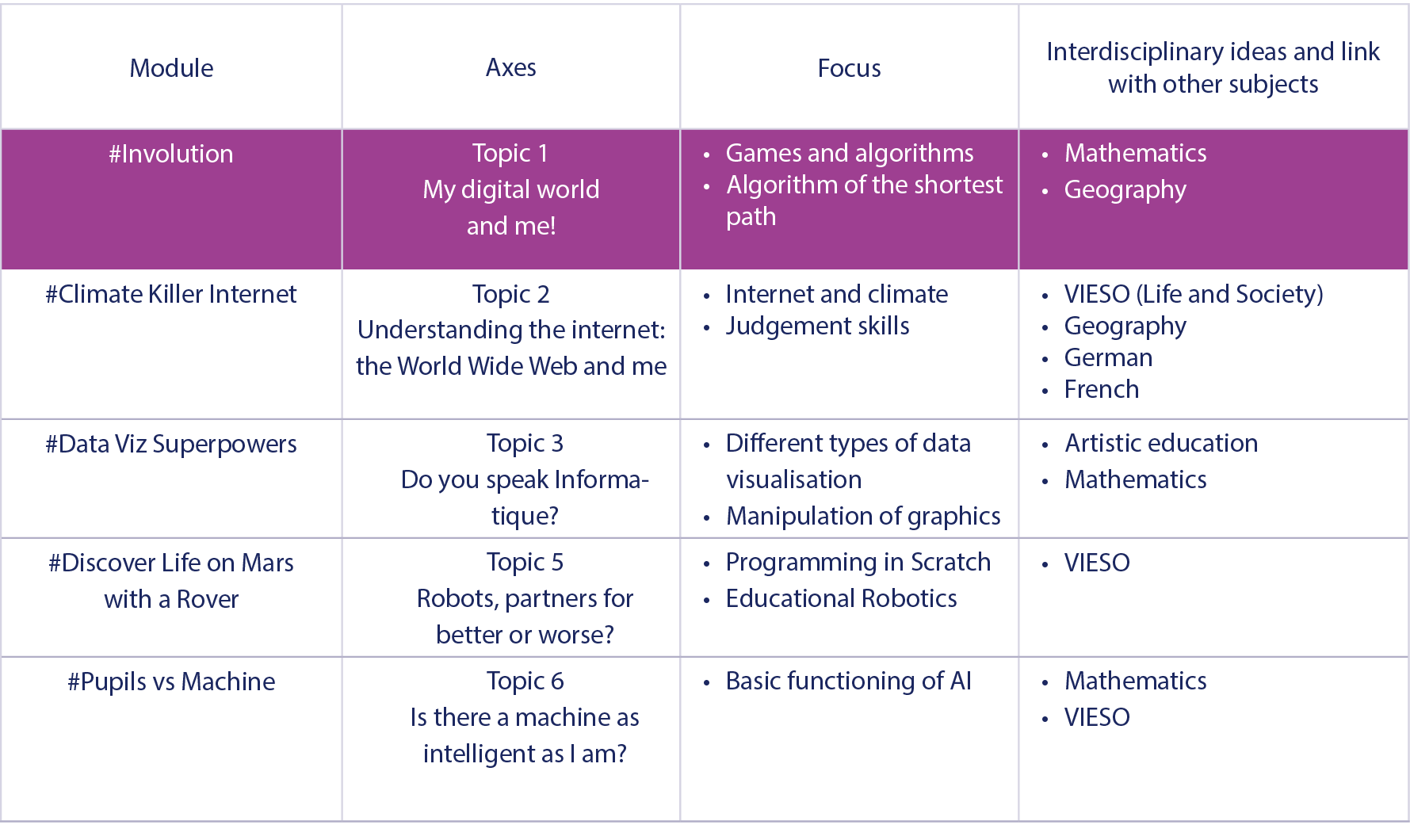
Since the modules are independent from each other, it is not necessary to be acquainted with the previous modules to tackle this one.
This module was devised in partnership with Hugo Parlier and Bruno Teheux from the Mathematics Department of the University of Luxembourg.
02
Conditions of unit
-
Target audience: 7e-5e (first to third year of classical and general secondary education)
-
Room: no specific premises required
-
Equipment required:
- The Involution© game: the game can be borrowed from the IFEN’s Centre of Pedagogical Documentation or the F.use (Future Spaces for Education) on the Belval Campus.
- Computers or tablets can be used to read the instructions or you can simply print the instructions.
4. Time: 2 hours of teaching time
03
Contextualisation of knowledge
The main objective of this lesson is to embody the notions of algorithm seen in class via Involution©: a game or puzzle developed by Hugo Parlier and Bruno Teheux, two mathematics researchers at the University of Luxembourg. Using this game, the pupils will familiarise themselves with mathematical and algorithmic concepts such as the shortest path algorithm and optimal and non-optimal strategies, all in a fun way. The game comprises a row of 10 black and white rings. A circular-shaped crank handle is placed on the game and the rings change position in a circular movement. The goal of the game is to change the position of the rings in order to get a given configuration based on the starting configuration.
04
Didactic transposition
a. Learning objectives and target skills
b. Didactic justification
c. Didactic reduction
Target skills in Topic 1: My Digital World and Me!
- KNOWLEDGE: a basic understanding of general computational and computer-related vocabulary, of human-computer communication (algorithmic notion) and of the abstraction principle when it comes to problem solving.
- KNOW-HOW: breaking down a problem in order to solve it, algorithm design and representation, simple algorithm production and application using maps and an operation sequence.
- SOFT SKILLS: an awareness of how computer science is involved in daily tasks based on the choice of tools, the information provided and the outcomes obtained.
Target skills in the Media Compass1
- Competence 2 – Communication and collaboration: 2.1. Working with others
- Competence 3 – Creating content: 3.3. Modelling, structuring and coding
The objective of this module is for pupils to gain an understanding of the notion of algorithms and how they work by way of a game. One of the module’s distinctive features is that the pupils are not to use electronic devices, computers or tablets. These so-called “unplugged” activities are often used to introduce computational thinking in order to “escape from the technological complexity of learning and to discover the fundamentals of computer science” (INRIA, 2020). This makes it easily accessible and enables pupils to understand a key area of digital technology: firstly, digital cultures do not have anything to do with computers in terms of electrical machines. The distinguishing feature of algorithmicity, for example, which is at the heart of this module, can be described as forming formal mathematical and logical models, which can also be represented in a mechanical way. To quote the computer scientist Leslie Lamport, “The importance of thinking and writing before you code needs to be taught in undergraduate computer science courses and it’s not” (Han, 2022).
Thus, the #Involution module is based on the foundations of coding taught in primary schools and builds on them, at the crossroads of mathematics and computer science.
Involution© poses several “shortest path” type challenges at different levels and places them within the cooperative learning and problem-solving framework. The game stimulates a targeted cognitive process which can be actively developed based on the teaching material handed out. When it comes to the planning and implementation of the teaching unit, a strict time limit can be completely disregarded in favour of a more freely experimenting with Involution© and the instructions provided. Knowledge and skills are consolidated through learning by teaching as the pupils will present their solutions and the reasons for their choices to the class.
05
Over the course of the lesson
In this module, the pupils play a game called Involution©. The game is made up of a tray with a crank handle. The tray has 10 holes that each contain one black or white ring.

A circle-shaped crank handle is placed on the game and the rings change position in a circular movement. The goal of the game is to change the position of the rings in order to reach a given configuration based on the starting configuration.
The game
The teacher briefly explains the principle of the game. The pupils are introduced to the game by simply playing it. They are split into pairs. Each group receives a box that contains a game tray (to be assembled) and challenge cards. Each card has two configurations. The challenge entails going from the configuration on the top to the configuration on the bottom by moving the crank handle. The pupils start by tackling the challenges in the given order. This activity is the first challenge in a long list of challenges in this module. All the challenges are provided in the teaching materials.
After this introduction, the pupils move on to the other challenges. The explanations below are for the same challenges. The module includes numerous challenges. The best-case scenario is that the pupils complete all the challenges. Starred challenges are more complicated (and more mathematical in their nature). They are designed for more eager pupils. Moreover, there are further optional challenges (as shown below in the detailed unit plan). Choosing not to take on these extra challenges will not impede the pupils from completing the module.
Challenge 2: After the initial stage, once the pupils have understood the principle of the game, they move on to challenge 2. The teacher divides the class in three groups; one group works on the first of three challenges; another works on the second and the final group on the third. The first challenge is slightly easier than the other two: please take this into account when dividing the class into groups and allocating the challenges.
Once the challenge has been solved, the pupils must agree among themselves, then communicate their solution to the rest of the class.
Challenge 3*: As the most complicated challenge, challenge 3 is optional. It should be taken on by eager pupils with a good level.
How to obtain all the configurations
This section helps pupils solve challenge 3. It concerns only the pupils who have tried it. Challenge 9 is one of the more demanding challenges in this section. We will leave it to the teacher to decide which pupils can/should take on the challenges in this section with or without challenge 9.
This section guides pupils towards solving challenge 3 using the mathematical principle of induction (without talking about the term itself or even mentioning it).
An optimal solution
Challenge 10: In challenge 10, the pupils look for a solution and count the number of movements they make to find that solution. They compare their solutions with each other.
In a moderated discussion, they come to the conclusion that one solution is better than another if it requires fewer movements.
A definition similar to the one below is formulated by the whole class:
A solution is optimal when it involves as few moves as possible.
The quest for an optimal solution
How do we find an optimal solution? Make the connection with the search for the shortest route in the New York underground, seen in Digital Sciences 1.
How to represent the game in graph form
This section starts with a more straightforward example: the Involution© game, but with only 5 rings and a reduced game tray. The 5 holes closest to the right must not be used. Therefore, there are only 2 possible positions in which to put the crank handle.
Challenge 11: The teacher divides the class in three groups. Within each group, the pupils are divided into pairs to play the game.
- The first group plays with 1 black ring (and 4 white rings).
- The second group plays with 2 black rings (and 3 white rings).
- The third group plays with 3 black rings (and 2 white rings).
The pupils try to solve their problem in pairs. Then they discuss it with their group and finally explain their outcome to the rest of the class.
Challenge 12*: This challenge is more complicated and is optional.
The pupils move on to the graph representation of the game (with the same game in a reduced format).
Challenge 13: For this challenge and those following it, the graph concept must be introduced or a brief reminder of it must be given. The pupils work in pairs, then they compare their results. They will find that the second and third cases are exactly the same. In a moderated discussion, the pupils will see that these two cases are symmetrical.
Challenge 14: Once the graph is constructed, challenge 12 becomes simpler. The pupils will see the answer clearly on the graphs.
In the next stage, the pupils repeat the game with 10 rings (5 black rings and 5 white rings).
Challenge 15*: This challenge is optional. The idea behind the challenge is to show the pupils that the counting exercises become complicated as the problem becomes more complex. Many pupils do not necessarily realise this because counting is very simple when only a few objects are involved.
The Involution© game’s graph representation is given, but it is too large to look for the shortest path with the naked eye.
The quest for an algorithm
To make the quest for an algorithm easier, the pupils move to 6 rings (3 black and 3 white). The 6-ring Involution© is small enough to search for the shortest path manually (contrary to the 10-ring Involution© graph), but large enough for the solution not to be ridiculous (contrary to the 5-ring Involution© graph).
Challenges 16 and 17: These challenges are used to put the pupils firmly on the track of an algorithm. These challenges are tackled in pairs. The outcomes are then discussed in class in the form of a moderated discussion.
Challenge 18: In this challenge, the algorithm is established manually. The pupils must write informal instructions. Point b) is more complex. It is intended for the most eager pupils only.
To draw the structural chart, the pupils can choose from drawing it from scratch or using the help already provided in the fields. The pupils must then put the fields in the right order and add arrows to form a structural chart.
Challenge 19: This challenge is only used to show the pupils that the general algorithm is exactly the same as those they have just done. This challenge is to be carried out directly in a moderated discussion.
Challenge 20: In a moderated discussion, the pupils realise that the algorithm they have just established is a shortest path algorithm. The same types of algorithms are used by GPS car navigators (see 1.6.02 The importance of graph theory in computational sciences).
06
Differentiation possibilities
For beginners
The module is completely feasible by dropping the starred challenges and sections. Encourage weaker pupils to do the module without these challenges.
For more eager pupils
Include the starred challenges (and the starred section) in exercises for more eager pupils. These challenges are slightly more mathematical in their nature and include logical reasoning. There is also a two-starred challenge. It is only intended for pupils with a good level and a decent grasp of the subject.
In challenges 2 and 11, the teacher can divide the pupils into three groups so that the pupils with the weakest level are given the most straightforward case to solve.
Challenge 18, that is to say the main challenge, where the algorithm is established, has three levels of difficulty:
- Establishing an algorithm that does only count the minimum number of movements and where the structure chart fields are already given.
- Same as above but without the structure chart fields.
- Establishing an algorithm that counts the minimum number of movements and the exact sequence of these movements
07
Further criteria to be met as part of the lesson series
-
The Luxembourgish context: the Involution© game was invented by Hugo Parlier and Bruno Teheux, two mathematics researchers from the University of Luxembourg. In its current form, the game can be linked to the contents in the Luxembourg Media Compass and it corresponds to the key topic I in Digital Sciences.
-
Differentiation: several of the module’s challenges are optional. The starred challenges are more complicated than the others and can be used (or not) depending on the level of the class and/or pupils.
-
Media Compass: see the learning objectives set out by the Media Compass in the teaching analysis section in this document.
-
The 4Cs model: communication, collaboration, creativity and critical thinking: the 4Cs model is applied in a range of ways through the different social forms and teaching activities.
-
Relation to current research: the challenges in Involution© are part of a family of reconfiguration problems (combinatorial reconfiguration), an area of research currently being studied in maths and computer science. The shortest path algorithms are more than 50 years old, but they remain the subject of research for the purpose of optimising shortest path applications.
-
Relation to research in Luxembourg: the Involution© game was developed by two researchers from the University of Luxembourg. In the podcast in section 1.7 A word from the scientists, Hugo Parlier explains how he develop games by using the results of his research.
08
Detailed planning of the lesson
Click on image to enlarge
Referenzen
Institut national de recherche en sciences et technologies du numérique (INRIA). (2020). Éducation et Numérique : enjeux et défis. Livre Blanc N 04. https://hal.inria.fr/hal-03051329v2/document
Han, Sheon. (2022). How to Write Software With Mathematical Perfection. Quantamagazine. https://www.quantamagazine.org/computing-expert-says-programmers-need-more-math-20220517
