Ann Kiefer

Pour être honnête, les mathématiciens ne font pas grand-chose. Ils boivent du café, froncent les sourcils devant les tableaux. Ils boivent du thé et froncent les sourcils devant les examens des étudiants. Ils boivent de la bière, froncent les sourcils devant les preuves qu’ils ont écrites l’année dernière et qu’ils n’arrivent plus à comprendre. C’est une vie où l’on boit, où l’on fronce les sourcils et, surtout, où l’on réfléchit. Vous voyez, il n’y a pas d’objets physiques en mathématiques : pas de produits chimiques à titrer, pas de particules à accélérer, pas de marchés financiers à détruire. Les verbes des mathématiciens se résument plutôt à des actions de pensée. […] les mathématiques sont une action de l’esprit.¹ Ceci est la description des mathématiciens et/ou des mathématiques donnée par B. Orlin (2018) dans son livre « Math with Bad Drawings: Illuminating the Ideas That Shape Our Reality ».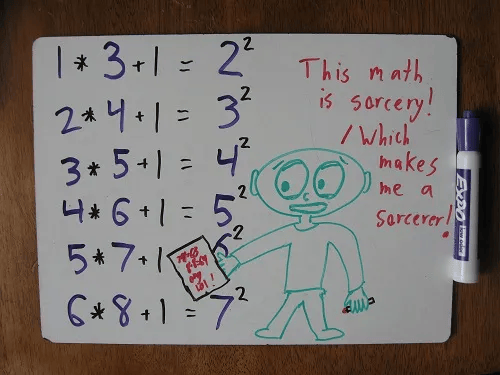

Source: Math with Bad Drawings: https://mathwithbaddrawings.com/2014/01/13/undiscovered-math/

Ce module donne la possibilité aux élèves de se plonger dans le rôle d’un mathématicien et d’explorer cet état d’esprit de penser mathématiquement. Mais c’est quoi exactement cette pensée mathématique ?

Les professeurs de musique incitent les élèves à écouter et à participer.
Les professeurs de langues et d’histoire invitent les élèves à voyager dans d’autres mondes.
Les professeurs d’art et d’art dramatique offrent aux élèves des possibilités d’exploration.

Que devons-nous offrir en mathématiques aux élèves pour qu’ils puissent fonctionner en mathématiques ? (Gilderdale, 2011)

Malheureusement, beaucoup de gens ont une idée fausse des mathématiques, les réduisant à de simples calculs ou multiplications de nombres. En réalité, les mathématiques sont une discipline profondément créative qui repose davantage sur la réflexion et l’expression écrite que sur l’arithmétique complexe que le grand public leur associe généralement.

Une équipe de recherche internationale (Petozc et al. 2007) a voulu savoir ce que les étudiants de première année à l’université entendaient par le terme « mathématiques ». L’enquête a été menée en Australie, au Brunei, au Canada, en Irlande du Nord et en Afrique du Sud (des pays ayant des liens historiques avec l’Empire britannique, et des systèmes éducatifs dérivant du système britannique). Ont été interrogés des élèves issus de filières de mathématiques, d’ingénierie et d’informatique. Un premier résultat : plus de la moitié des étudiants ont défini les mathématiques avant tout comme un outil permettant de trouver des solutions à des problèmes. Les auteurs en concluent qu’il est urgent d’élargir le champ des mathématiques et de donner aux étudiants une image plus large des mathématiques. Les chercheurs proposent que les enseignants ne se concentrent pas uniquement sur les techniques dans les cours et les salles de classe, mais qu’ils montrent comment certaines professions utilisent et comprennent les mathématiques (professeurs de mathématiques, statisticiens, ingénieurs, programmeurs, etc.). Pour ces professions aussi, les chiffres et les boîtes à outils font partie intégrante des mathématiques. Mais ce n’est que le début pour eux.

Nous nous sommes donnés pour but de commencer cette ouverture d’esprit sur les mathématiques plus tôt qu’à l’université et l’un des objectifs de ce module est de montrer ce qu’est réellement la pensée mathématique, la résolution de problèmes et la rédaction de preuves, de montrer comment faire ces choses, et de montrer à quel point c’est amusant. Dans ce module nous donnons (essayons de donner) une réponse à cette question en brisant avec la structure classique d’un cours de mathématique, où l’enseignant explique la théorie, fait un exemple au tableau devant toute la classe et puis les élèves répètent le même exemple plusieurs fois en version « drill ». Ici les élèves reçoivent comme point de départ quelques exemples qui illustrent une curiosité mathématique. Puis c’est aux élèves de trouver plus d’exemples eux-même et de dégager un shéma récurrent derrière ces exemples pour ensuite formuler une conjecture. Une fois leur conjecture formulée, ils doivent essayer de la prouver ou de trouver un contre-exemple. Tout ce travail est effectué en groupe, suivi par des mises en commun et des discussions en classe. Le leitmotiv serait ici HOTS not MOTS, où HOTS est l’abréviation de High Order Thinking Skills et MOTS est l’abréviation de More Of The Same. Cette activité permettra aux élèves de vivre l’expérience authentique d’un mathématicien professionnel. Contrairement aux exercices traditionnels, ils devront explorer, analyser et tenter de prouver ou réfuter un théorème en s’appuyant sur des observations intrigantes faites précédemment.

Le module « Dans la peau d’un∙e mathématicien∙ne » devrait être utilisé dans le chapitre calcul littéral du programme de 6^e et vise la modélisation d’une situation à l’aide d’une expression littérale. Cette activité stimule la capacité des élèves à se poser les bonnes questions et à « penser mathématiquement ». Le concept de pensée mathématique n’est pas nouveau. Pólya était un des premiers mathématiciens à décrire comment résoudre des problèmes mathématiquement (Pólya, 1945). Schoenfeld (1985, 1992) a étendu ensuite ces idées fondamentales en identifiant plusieurs composantes de la pensée mathématique : la base de connaissances, les stratégies de résolution de problèmes, la métacognition (contrôle et autorégulation) et les systèmes de croyance. Pour le dire dans les mots de Stein et Smith (1998) :

Les tâches qui demandent aux élèves d’exécuter une procédure mémorisée de manière routinière constituent un type d’opportunité pour la réflexion des élèves ; les tâches qui exigent des élèves une réflexion conceptuelle et qui les incitent à établir des liens constituent un ensemble différent d’opportunités pour la réflexion des élèves.

C’est aussi le constat de David Baker, professeur de sociologie et éducation à l’Université de Pennsylvania : Dans l’ensemble, on observe une évolution vers des mathématiques cognitives plus complexes, une évolution qui invite l’élève à agir comme un mathématicien au lieu d’assimiler passivement les mathématiques et les sciences.²

Ceci n’est bien-sûr pas un exercice facile, ni pour l’élève, ni pour l’enseignant. Les difficultés à comprendre, à faire des connexions et à expliquer, que les élèves rencontreront lors de cette activité, sont désignées par Schoenfeld (2023) par le terme de lutte positive (positive struggle). Il s’agit d’un mécanisme permettant de développer une compréhension profonde et significative du contenu mathématique.

Du point de vue des enseignants, ceux-ci doivent être curieux, intrigués et désireux d’en savoir plus, mais aussi accepter le travail désordonné, valoriser la prise de risque et les idées à moitié formées, donner du temps pour réfléchir et encourager la discussion (Gilderdale, 2011). Le plus important reste cependant que les enseignants choisissent bien les sujets et les groupes d’élèves afin que tout le monde puisse profiter de l’activité et développer ses capacités de pensé mathématique.

Le module « Dans la peau d’un∙e mathématicien∙ne » est un bon exemple aussi d’une activité TRU. L’acronyme TRU signifie Teaching for Robust Understanding et est un cadre fondé par Alan H. Schoenfeld, professeur à l’Université de Californie. Il décrit les propriétés des salles de classe dans lesquelles les élèves deviennent des penseurs puissants et autonomes en mathématiques (Schoenfeld, 2023). Les cinq dimensions de l’activité en classe sont au cœur du TRU. Les salles de classe qui réussissent bien dans ces 5 dimensions produisent des élèves qui sont des penseurs puissants :

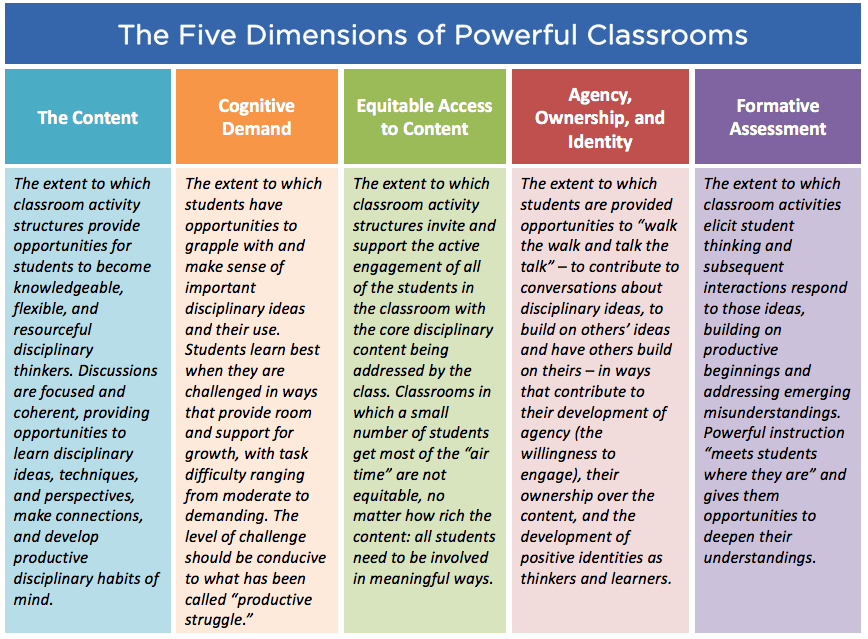
Source: Le cadre de l’TRU en bref, https://truframework.org/

En résumé ce module a pour but de montrer aux élèves le côté abstrait, mais aussi créatif et curieux des mathématiques. Nous espérons de changer l’image des mathématiques ennuyeuses, ne servant à rien et loin de la réalité, contre une image plus positive et passionnante.

Je ne m’attends pas, et je ne veux pas, que tous les enfants trouvent que les mathématiques sont une étude passionnante, ou une étude à laquelle ils veulent se consacrer, que ce soit à l’école ou dans leur vie. Seuls quelques-uns d’entre eux trouveront les mathématiques suffisamment séduisantes pour s’y engager à long terme. Mais j’espère que tous les enfants pourront faire l’expérience, à quelques moments de leur carrière, de la puissance et de l’enthousiasme des mathématiques, de sorte qu’à la fin de leur éducation formelle, ils sauront au moins à quoi elles ressemblent et si c’est une activité qui a sa place dans leur avenir.³

Quelques-uns feront le reproche à ce module qu’il est trop abstrait et ne montre pas le côté appliqué des mathématiques. À ceux-là nous répondons que d’autres modules de ce PITT font déjà ce travail et, plus important, nous insistons sur le fait que les mathématiques ne sont pas seulement enseignées parce qu’elles sont utiles. Elles devraient être une source de plaisir et d’émerveillement, offrant aux élèves une excitation intellectuelle et une appréciation de leur créativité essentielle.⁴

¹ To be honest, mathematicians don’t do much. They drink coffee, frown at chalkboards. Drink tea, frown at students’ exams. Drink beer, frown at proofs they wrote last year and can’t for the life of them understand anymore. It’s a life of drinking, frowning, and, most of all, thinking. You see, there are no physical objects in math : no chemicals to titrate, no particles to accelerate, no financial markets to destroy. Rather the verbs of the mathematicians all boil down to actions of thought. […] mathematics is an action of the mind (B. Orlin, 2018)

² Overall, there’s a movement towards more complex cognitive mathematics, there’s a movement towards the student being invited to act like a mathematician instead of passively taking in math and science. (Hartnett, 2016)

³ I don’t expect, and I don’t want, all children to find mathematics an engrossing study, or one that they want to devote themselves to either in school or in their lives. Only a few will find mathematics seductive enough to sustain a long term engagement. But I would hope that all children could experience at a few moments in their careers…the power and excitement of mathematics…so that at the end of their formal education they at least know what it is like and whether it is an activity that has a place in their future. (Wheeler, D. (1975), cité dans Cross, K. (2004))

⁴ Mathematics is not only taught because it is useful. It should be a source of delight and wonder, offering pupils intellectual excitement and an appreciation of its essential creativity. (Cross, 2004)

Références

1. Cross, K. (2004). Engagement and excitement in mathematics. Mathematics Teaching. Vol. 189, pp. 4-7
2. Gilderdale, C. (2011). Generating Curiosity in Mathematics Learning. Nrich. https://nrich.maths.org/5795
3. Hartnett, K. (2016). Meet the New Math, Unlike the Old Math. Quantamagazine. https://www.quantamagazine.org/math-and-science-education-pencils-down-20161005/ 
4. Orlin, B. (2018). Math with Bad Drawings: Illuminating the Ideas That Shape Our Reality. ‎ Black Dog & Leventhal; Illustrated edition.
5. Petocz, P., Reid, A., Wood, L.N., Smith, G.H., Mather, G., Harding, A., Engelbrecht, J., Houston,K., Hillel, J., and Perrett, G. (2007) Undergraduate students’ conceptions of mathematics: an international study. International Journal of Science and Mathematics Education: 5: 439-459
6. Pólya, G. (1945). How to Solve It (2nd edition). Princeton: Princeton University Press.
7. Schoenfeld, A.H. (1985). Mathematical problem solving. Orlando, FL: Academic Press.
8. Schoenfeld, A.H. (1985). Learning ot think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. Grouws (Ed.), Handbook for research on mathematics, teaching and learning, pp. 334-370. New York: MacMillan.
9. Schoenfeld, A.H. (2023). Helping Students Become Powerful Mathematics Thinkers : Case Studies of Teaching for Robust Understanding. New York: Routledge.
10. Stein, M.K. & Smith, M.S. (1998). Mathematical tasks as a framework for reflection. Mathematics Teaching in the Middle School, 3, 268-275.