Comment savoir si quelque chose est vrai ou non ? On vous a certainement déjà dit que la somme des angles d’un triangle est égale à 180° par exemple, mais comment en être sûr ? Et si vous rencontriez un extraterrestre qui n’a jamais étudié la géométrie de base ? Comment pourriez-vous le convaincre que ce fait est vrai ? D’une certaine manière, c’est là tout l’enjeu des mathématiques : concevoir de nouvelles affirmations, décider d’une manière ou d’une autre si elles sont vraies ou fausses, et expliquer ces résultats à d’autres personnes (ou extraterrestres, selon le cas).

En passant, vous pourriez même vous demander « Qu’est-ce que cela signifie pour quelque chose d’être vraie ? » Une discussion complète sur cette question devrait plonger dans la philosophie, la psychologie, et peut-être la linguistique, et nous ne voulons pas vraiment entrer dans ces domaine (pour plus d’inspiration, consultez la section 1.4 Idées interdisciplinaires). L’idée principale, dans le contexte des mathématiques, est que quelque chose n’est vrai que si l’on peut démontrer qu’elle est toujours vraie. Nous savons que 1+1=2 toujours et pour toujours. Qu’il soit minuit ou midi, nous pouvons être sûrs que cette équation restera vraie. (Avez-vous déjà réfléchi à la façon de démontrer un tel fait ? C’est en fait assez difficile ! Un livre intitulé Principia Mathematica (Whitehead & Russell, 1997) aborde cette question à partir des « premiers principes » et il faut aux auteurs de nombreuses pages pour arriver à 1+1=2). Ceci est très différent d’autres sciences. Si nous réalisons une expérience physique 10 fois et que le même résultat se produit, savons-nous qu’il en sera toujours ainsi ? Et si nous réalisons l’expérience un million de fois ? Un milliard ? À quel moment avons-nous réellement prouvé quelque chose ? En mathématiques, l’expérimentation répétée n’est pas une preuve viable ! Il faudrait trouver un argument qui montre pourquoi un tel phénomène se produirait toujours. À titre d’exemple, la conjecture 13 de ce modèle est un célèbre problème ouvert appelé conjecture de Goldbach. On ne sait pas encore si elle est vraie ou non, même si elle a été vérifiée par des simulations informatiques jusqu’à une valeur d’environ 10¹⁸. C’est un nombre énorme, mais il n’est pas encore suffisant pour savoir si la conjecture est vraie ou fausse. Voyez-vous la différence ? Les mathématiciens aiment prouver des faits. Le fait de vérifier un certain nombre de valeurs, mais pas toutes, ne constitue pas une preuve.¹

La preuve est donc ce qui rend les mathématiques différentes des autres sujets et ce qui caractérise les mathématiques. Si nous étions dans la Grèce antique, la science la plus récente nous dirait que quatre éléments composent toutes les choses : le feu, l’eau, la terre et l’air. Elle nous dirait aussi que dans un triangle rectangle le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. Aujourd’hui nous croyons toujours un des deux faits, mais plus l’autre. La différence entre les deux : le théorème de Pythagore a été prouvé (Hart, 2024). Et un théorème qui a été prouvé une fois en mathématiques, même si sa preuve est vieille de plusieurs milliers d’années, restera vrai pour toujours. C’est là la grande différence entre les mathématiques et les autres sciences naturelles.

Une fois qu’il existe une preuve valide d’un théorème, cela suffit, en termes purement mathématiques. Il n’est pas nécessaire de le prouver à nouveau, et cela ne le rend pas « plus vrai ». Alors pourquoi certains résultats ont-ils de nombreuses preuves ? Le théorème de Pythagore en est un exemple. Avec des centaines de preuves, il est peut-être le théorème le plus prouvé de tous les temps. Plusieurs raisons expliquent cette multiplicité de preuves. Tout d’abord, le théorème a été remarqué dans de nombreuses cultures différentes. Même l’Égypte ancienne, qui ne connaissait probablement pas le résultat général, semble avoir su et utilisé le fait qu’un triangle 3-4-5 a un angle droit opposé au côté le plus long. Plus tard, dans les traditions grecque, indienne et chinoise, on trouve différentes preuves. Mais même lorsque les preuves du résultat étaient bien connues, les gens continuaient à en trouver de nouvelles. Dans le cas du théorème de Pythagore, il s’agit en quelque sorte d’un passe-temps mathématique, mais il arrive que la découverte d’une autre preuve d’un résultat permette de montrer des liens qui n’avaient pas été remarqués auparavant ou des généralisations potentielles. Parfois, en utilisant une nouvelle technique, on se rend compte que celle-ci peut être appliquée plus largement. En outre, il arrive souvent que la première preuve d’un théorème ne soit pas la meilleure – elle fait le travail, à voire prouver le résultat, mais des personnes ultérieures trouvent des arguments plus clairs et des chemins plus courts. Au fil des ans, les preuves peuvent être affinées et simplifiées, de sorte qu’il ne reste finalement qu’un beau noyau cristallin où le génie exquis de l’idée sous-jacente est mis en valeur (Hart, 2024). Considérons le problème 09 de ce module : à première vue il paraît que \(n^2+n+41 \) est toujours premier pour n’importe quel n. En tout cas, l’expression est un nombre premier pour n=0,1,2,3,4,5,6,7,8,9,10. Est-ce qu’elle donne donc toujours un nombre premier. La réponse est non (voir 1.7 Solutions). Une première preuve de ceci pourrait être de simplement tester toutes les valeurs de n les unes après les autres et de se rendre compte qu’en n=40, l’expression donne 1681 qui n’est pas premier, car 1681 est divisible par 41. Une manière rapide de voir cette divisibilité (sans utilisation d’outils technologiques) est le calcul suivant :

Ceci constitue certes une preuve mathématique complètement correcte, mais elle n’est pas très élégante. Une preuve plus élégante est de voir que si on prend n=41, on obtient une somme de 3 termes dont chacun est divisible par 41 (la somme étant 41^2+41 +41) et donc toute l’expression est divisible par 41 et ne donne donc pas un nombre premier. Pour voir plus d’exemples de preuves élégantes, nous conseillons aux lecteurs de regarder la conférence A Mathematician’s View of a Proof donnée par la mathématicienne anglaise Sara Hart.

¹ Ce texte est la traduction du début du livre Everything You Always Wanted To Know About Mathematics (https://ia600408.us.archive.org/26/items/everything-you-always-wanted-to-know-about-mathematics/bws_book.pdf) que nous recommandons fortement aux lecteurs. 

« Les mathématiques sont un sujet vaste, en perpétuelle croissance et en constante évolution. Parmi les innombrables questions que les mathématiciens se posent, et auxquelles ils répondent pour la plupart, certaines se distinguent des autres : des pics proéminents qui dominent les charmants contreforts. Ce sont les vraies grandes questions, les problèmes difficiles et ardus, pour lesquels n’importe quel mathématicien donnerait son bras droit pour pouvoir résoudre. Certaines de ces questions sont restées sans réponse pendant des décennies, d’autres pendant des siècles, quelques-unes pendant des millénaires. D’autres n’ont pas encore été résolues. »² C’est ainsi que commence le livre The Great Mathematical Problems écrit par Ian Stewart (Stewart, 2014).

Le Dernier Théorème de Fermat

Un des problèmes les plus connus est le Dernier Théorème de Fermat. Le mathématicien français Pierre de Fermat a énoncé ce théorème dans une note marginale de son exemplaire du livre Arithmétiques de Diophante au 17^e siècle. À un endroit de ce livre, les triplets Pythagoriciens sont traités. Dans la marge, Fermat écrit :

Au contraire, il est impossible de partager soit un cube en deux cubes, soit un bicarré en deux bicarrés, soit en général une puissance quelconque supérieure au carré en deux puissances de même degré : j’en ai découvert une démonstration véritablement merveilleuse que cette marge est trop étroite pour contenir.

L’énoncé mathématique moderne est le suivant :

Dernier théorème de Fermat. Pour tout entier n>2, il n’existe pas de triplet d’entiers strictement positifs (x,y,z) tels que l’équation suivante soit satisfaite :

Les solutions triviales correspondent aux cas où l’un des termes est nul. Pendant plus de trois siècles, ce théorème est resté sans preuve.

Dans l’épisode Treehouse of Horrors VI de la série The Simpsons, on trouve une référence à ce fameux théorème de Fermat.

Si l’équation derrière Homer Simpson était vraie, un contre-exemple au Dernier Théorème de Fermat aurait été trouvé. En calculant, on trouve que le côté gauche vaut

2541210258614589…

alors que le côté droit vaut

2541210259314801…

Les deux nombres ont 40 chiffres et leur 9 premiers chiffres sont les mêmes. Cependant, on voit très rapidement, sans calcul, que cette équation ne peut pas être correcte car le côté gauche est un nombre impair alors que le côté droite est un nombre pair.

De nombreux mathématiciens ont tenté de le démontrer, mais sans succès. Ce n’est qu’en 1994 que le mathématicien britannique Andrew Wiles a réussi à prouver ce théorème en utilisant des concepts avancés de la théorie des nombres et de la géométrie algébrique, notamment les courbes elliptiques et les formes modulaires. L’histoire derrière le mathématicien Wiles est impressionnante aussi. À l’âge de 10 ans, Andrew Wiles découvrit le Dernier Théorème de Fermat, une énigme mathématique vieille de plusieurs siècles. Cette rencontre marqua un tournant dans sa vie, et il fit le serment de devenir mathématicien plus tard et de résoudre ce mystère un jour. Pendant ses études en mathématiques, Wiles se spécialisa dans la théorie des nombres, une branche qui abritait ce fameux théorème. Cependant, plus il s’immergeait dans les arcanes des mathématiques, plus il percevait la complexité insaisissable du problème. Le théorème semblait hors de portée, et il abandonna temporairement son ambition. Mais le destin réserve parfois des surprises. D’autres mathématiciens firent le lien entre le Dernier Théorème de Fermat et les courbes elliptiques ainsi que les formes modulaires, des sujets dans lesquels Wiles était devenu un expert entre-temps. Pendant sept années intenses et secrètes, Wiles se consacra corps et âme à la preuve. En 1994, lors d’une série d’exposés, Wiles révéla enfin sa preuve au monde. L’annonce fit sensation, même dans les médias grand public, un événement rare pour une démonstration mathématique.

Ainsi, le Dernier Théorème de Fermat, qui avait hanté les esprits pendant des siècles, trouva enfin sa réponse grâce à la ténacité et à l’ingéniosité d’Andrew Wiles. La preuve de Wiles a eu un impact profond sur les mathématiques. Elle a ouvert de nouvelles perspectives dans la théorie des nombres et a renforcé notre compréhension des courbes elliptiques et des formes modulaires. Le Dernier Théorème de Fermat est désormais un exemple emblématique de la puissance des mathématiques et de la persévérance des chercheurs (Stewart, 2014). Pour une histoire plus étendue du Dernier Théorème de Fermat, nous recommandons le livre incroyable de Simon Singh, intitulé Fermat’s Last Theorem (Singh, 2002). Un joli résumé de l’histoire du Dernier Théorème de Fermat est aussi fait dans les 30 premières minutes du podcast Dernier Théorème de Fermat : à l’épreuve de l’informatique de la série La Science, CQFD de France Culture, mentionné à la fin de la section 03 Et l’intelligence artificielle dans tout ça ?

La conjecture de Kepler

Une autre conjecture connue qui a mis plusieurs centaines d’années à être résolue est la conjecture de Kepler. En 1611, l’astronome Johannes Kepler, qui avait commencé à étudier les arrangements de sphères, énonça sa conjecture :

Conjecture de Kepler. Pour un empilement de sphères égales, en espace libre, la densité maximale est atteinte pour un empilement compact de plans compacts.

Pour expliquer ceci de manière plus simple, considérons un grand espace vide, tel qu’un hangar d’aviation, et demandons-nous quel est le plus grand nombre de boules que l’on peut y placer. Si, au lieu de boules, nous essayons d’empiler des cubes de bois identiques, comme les blocs de construction pour enfants, la réponse devient facile. Les cubes s’emboîtent les uns dans les autres sans espace perdu et nous pouvons remplir pratiquement cent pour cent de l’espace (en ignorant la petite quantité d’espace qui peut rester autour des murs et au plafond), et donc le nombre de cubes que nous pouvons empiler est presque égal au volume du hangar divisé par le volume de l’un des cubes.

Mais les sphères ne s’emboîtent pas aussi bien que les cubes, et il y a toujours de l’espace perdu entre les deux. Quelle que soit l’ingéniosité avec laquelle les boules sont disposées, environ un quart de l’espace ne sera pas utilisé. Une disposition familière est la suivante :

Source: Source : Empilement compact de plans compact (Conway & Sloane, 1999)

Et c’est en 1611 que Kepler prétendait que c’est aussi l’empilement le plus optimal qui existe. Il en était convaincu mais n’arriva pas à le prouver. C’est seulement en 1998 que Thomas Hales annonça avoir démontré la conjecture. Sa preuve était très longue et assistée par ordinateur. Elle était extraordinairement difficile à vérifier, mais est aujourd’hui complètement vérifiée et acceptée par la communauté mathématique. L’histoire ne s’arrêta pas là car la question d’un empilement optimal de sphère peut se poser dans n’importe quelle dimension (et pas seulement en dimension 3). Ce problème plus général est connu sous le nom de Sphere Packing Problem. La solution optimale en dimension 2 est la suivante :

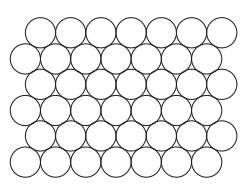
L’empilement optimal en dimension 2 n’a seulement été démontré qu’en 1940. Pour les dimensions supérieures, le problème a été résolu récemment pour les dimensions 8 et 24 par la mathématicienne russe Maryna Viazovska (Klarreich, 2016).

Source: : https://www.faz.net/aktuell/wissen/falling-walls/die-mathematikerin-maryna-viazovska-gewinnerin-der-fields-medaille-im-gespraech-18452365.html/

Pour toutes les autres dimensions (dimensions strictement supérieures à 3 et différentes de 8 et 24), l’empilement optimal n’est pas encore connu.

La conjecture des nombres premiers jumeaux

Une troisième conjecture de laquelle on voulait parler est la conjecture des nombres premiers jumeaux.

Définition. Soient \(p_1\) et \(p_2\) deux nombres premiers. On dit que \(p_1,p_2\) forme un couple de nombres premiers jumeaux si 

\[ p_2-p_1=2. \]

Les premiers couples de nombres premiers jumeaux sont

(3,5),(5,7),(11,13),(17,19),…

Nous savons depuis Euclide (300 av. J-Chr.) qu’il y a une infinité de nombres premiers. La question qui se pose alors, et que les mathématiciens se posent depuis le 19e siècle, est s’il y a aussi une infinité de nombres premiers jumeaux. Comme la preuve de l’infinité des nombres premiers est relativement simple, les mathématiciens croyaient au début que la preuve de l’infinitude des nombres premiers jumeaux ne pourrait pas être très compliquée non plus. Mais personne n’arrivait à trouver une preuve. Certes, les ordinateurs trouvaient des nombres premiers jumeaux de plus en plus grands. Les plus grands connus à ce jour sont

Ils ont été découverts en 2016. Nous savons aussi qu’il y a 808.675.888.577.436 nombres premiers jumeaux avec moins de 18 chiffres. Tous ces faits font que les mathématiciens sont convaincus qu’il y a bel et bien un nombre infini de nombres premiers jumeaux. Or comme nous avons vu au paragraphe précédent, être convaincu ou trouver un grand nombre d’exemples qui fonctionnent ne constitue pas une preuve en mathématique. En mai 2013 tout a changé avec la publication d’un article du mathématicien Yitang Zhang. Dans l’article il a démontré le théorème suivant.

Théorème (Zhang, 2013). Il y a une infinité de nombres premiers  \(p_1,p_2\) tels que
\[ p_2-p_1 \leq 70.000.000. \]

Ce théorème a fait sensation dans le monde mathématique. Pourquoi ? En fait, jusqu’en 2013 rien n’était connu au sujet des nombres premiers jumeaux. Les mathématiciens étaient convaincus de leur infinitude, mais ils n’avaient aucune preuve. Donc, il se pourrait que les nombres premiers s’écartent de plus en plus : qu’après un certain nombre énorme, on ne trouve plus de nombres premiers jumeaux, et puis après un nombre encore plus énorme, on ne trouve plus de nombres premiers d’écart 4, et puis d’écart 6 etc. C’était une réelle possibilité. En 2013, Zhang démontra que si nous nous donnons comme limite supérieure le nombre 70.000.000, alors on trouvera toujours des nombres premiers écartés d’au plus 70.000.000 aussi loin qu’on aille sur la ligne des nombres. Soyons d’accord, 70.000.000 n’est pas du tout égal à 2 mais les deux nombres ne sont pas si différents non plus, dans le sens que ce théorème de Zhang était un premier pas dans la bonne direction. Dans l’année qui suivit, plusieurs autres mathématiciens, dont Terrence Tao (voir section suivante), ont réussi à réduire le nombre de 70.000.000 à 246 ce qui donne comme théorème actuel :

Théorème (Maynard, Polymath, Tao, 2014). Il y a une infinité de nombres premiers  \(p_1,p_2\) tels que
\[ p_2-p_1 \leq 246. \]

La limite 246 est déjà plus proche de 2 que la limite antérieure, mais malheureusement Tao et Maynard ont démontré aussi qu’avec les méthodes appliquées jusqu’à présent, il sera impossible de réduire plus cette limite. Il faudra donc trouver une nouvelle idée ou des nouvelles méthodes mathématiques ce qui fait qu’une avancée a certes eu lieu dans la conjecture des nombres premiers jumeaux, mais la conjecture reste ouverte.

D’autres conjectures ouvertes connues sont celles illustrées dans les problèmes 13 et 14 de ce module.

La conjecture de Goldbach

Le problème 13 est connu sous le nom de la conjecture de Goldbach, formulée en 1742 par Christian Goldbach.

Conjecture de Goldbach. Tout nombre entier pair supérieur à 3 peut s’écrire comme une somme de deux nombres premiers.

C’est l’une des plus vieilles conjectures ouvertes en mathématiques. Elle est vérifiée pour tout nombre pair inférieur à \(4 \cdot 10^{18} \), mais reste ouverte en général. Il existe une version faible de la conjecture de Goldbach, qui dit que tout nombre pair supérieur à 9 s’écrit comme somme de trois nombres premiers. Cette version s’appelle version faible, car si la conjecture de Goldbach sera démontrée un jour, la version faible en découle tout de suite : en effet, chaque nombre pair a supérieur à 9, s’écrit comme la somme d’un nombre pair b et de 3. Du coup si b s’écrit comme somme de deux nombres premiers (par la conjecture de Goldbach), a s’écrit comme somme de ces deux nombres premiers et 3, donc de 3 nombres premiers.

En 2013, le mathématicien péruvien Harald Helfgott avait publié une preuve de la version faible. Cette preuve n’est toujours pas vérifiée.

Source: xkcd https://xkcd.com/1310//

Terrence Tao, que nous avons déjà rencontré plusieurs fois, a prouvé le théorème suivant.

Théorème (Tao, 2012). Tout nombre entier impair supérieur à 5 peut s’écrire comme une somme de trois nombres premiers.

La conjecture de Goldbach fait partie du problème 8 des problèmes de Hilbert, ensemble avec la conjecture des nombres premiers jumeaux et l’hypothèse de Riemann. L‘hypothèse de Riemann est probablement la conjecture la plus connue en mathématique. Cette hypothèse d’apparence anecdotique avancée par Bernhard Riemann il y a cent cinquante ans porte sur sujet de la répartition des nombres premiers. Un aperçu passionnant et compréhensible en est donné dans le livre The Music of the Primes du mathématicien Marcus du Sautoy (du Sautoy, 2003). La vidéo suivante en présente une très brève synthèse.

Lors du deuxième congrès international des mathématiciens, qui s’est tenu à Paris en août 1900, David Hilbert a présenté une liste de problèmes qui avaient jusqu’alors posé des défis aux mathématiciens. Selon Hilbert, ces problèmes devaient marquer l’évolution des mathématiques au XXe siècle, et il est indéniable qu’ils ont eu un impact considérable. Après la tenue du congrès, la liste définitive comprenait 23 problèmes, aujourd’hui connus sous le nom de problèmes de Hilbert. Aujourd’hui 8 de ces problèmes sont complètement résolus, 10 ont des solutions partielles et 5 sont encore sans solution. Une anecdote drôle est que Hilbert exprima des opinions quelque peu contradictoires concernant la difficulté de l’hypothèse de Riemann. À un moment donné, il a comparé trois problèmes non résolus : la transcendance de \(2^{\sqrt{2}}\), le Dernier Théorème de Fermat et l’hypothèse de Riemann. Selon lui, l’Hypothèse de Riemann serait probablement résolue dans quelques années, le dernier théorème de Fermat peut-être de son vivant, et la question de la transcendance peut-être jamais. Étonnamment, la question de la transcendance a été résolue quelques années plus tard. Comme vu auparavant, Andrew Wiles a récemment prouvé le Dernier Théorème de Fermat et l’hypothèse de Riemann reste ouverte. Une autre fois, Hilbert a fait remarquer que s’il se réveillait après un sommeil de cinq cents ans, sa première question serait de savoir si l’hypothèse de Riemann avait été résolue (Conray, 2003).

L’équivalent des problèmes de Hilbert au 21^e siècle est la liste des sept problèmes du prix du millénaire sélectionnés en 2000 par l’Institut de mathématiques Clay. Contrairement aux problèmes de Hilbert, pour lesquels la principale récompense était l’admiration de David Hilbert lui-même et des mathématiciens en général, chaque problème du prix est assorti d’une prime d’un million de dollars. À ce jour, seulement un des sept problèmes a été résolu. C’est la conjecture de Poincaré qui a été résolue par le mathématicien excentrique russe Grigori Perelman.

La conjecture de Collatz

Le problème 14 de ce module, est connu dans le monde mathématique sous le nom de conjecture de Collatz ou conjecture de Syracuse. Cette conjecture ne fait pas partie des grands problèmes mathématiques mais est entrée dans le folklore mathématique car malgré la simplicité de son énoncé (on peut l’expliquer à un enfant de primaire), cette conjecture défie depuis de nombreuses années les mathématiciens.

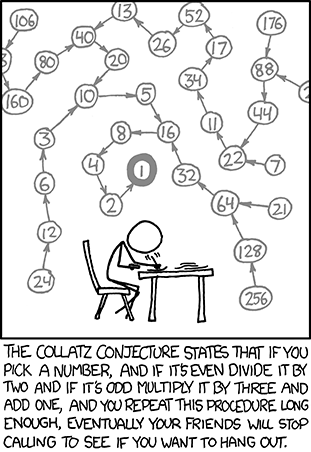
La vidéo suivante de Derek Muller de la chaîne de Youtube Veritasium en donne plus d’informations.

La conjecture d’Euler

Tout comme dans ce module, il y avait aussi dans l’histoire des mathématiques des conjectures dont les mathématiciens étaient convaincus qu’elles soient vraies et qui se sont révélées fausses pour finir. Un exemple connu en est la conjecture d’Euler qui a été originellement proposée par le mathématicien suisse Leonhard Euler en 1772 et qui s’énonce de la façon suivante :

Conjecture d’Euler. Pour tout entier n strictement supérieur à 2, la somme de n – 1 puissances
n-ièmes n’est pas une puissance n-ième.

Remarquons que le cas n=3 correspond au Dernier Théorème de Fermat avec exposant 3. C’est seulement en 1966 que deux mathématiciens trouvent un contre-exemple et écrivent un des articles les plus courts qui n’ont jamais été publiés en mathématique :

Source:https://www.ams.org/journals/bull/1966-72-06/S0002-9904-1966-11654-3/S0002-9904-1966-11654-3.pdf/

La conjecture de Pólya

Un dernier exemple de conjecture réfutée est la conjecture de Polya . Nous allons commencer par une définition.

Définition. Un nombre entier positif est appelé de type pair si sa factorisation en nombres premiers contient un nombre pair de facteurs premiers. Sinon il est appelé de type impair.

Faisons un exemple. Comme \(15=3 \cdot 5\), 15 possède 2 facteurs premiers et est donc de type pair. Par contre \(12=2\cdot 2 \cdot 3 \) et donc 12 est de type impair.

Par définition, 1 est de type pair et tous les nombres premiers sont de type impair.

Définition. On désigne par E(n) le nombre d’entiers positifs inférieurs ou égaux à n qui sont de type pair et par O(n) le nombre d’entiers positifs inférieurs ou égaux à n qui sont de type impair.

Essayons de déterminer E(9) et O(9). On prend tous les nombres entiers positifs de 1 à 9 inclus, puis on décide s’ils sont de type pair ou de type impair.

• Les nombres 1,4,6 et 9 sont de type pair. Il y en a 4 en tout. Donc E(9)=4.
• Les nombres 2, 3, 5, 7 et 8 sont de type impair. Il y en a 5 en tout. Donc O(9)=5.

Conjecture de Polya. Pour tout entier \(n \geq 2 \), E(n) est inférieur ou égal à O(n).

Existe-il une preuve pour la conjecture de Polya ?
La réponse c’est … non !

En 1962, Sherman Lehman a trouvé que cette conjecture échoue pour n=906 180 359. Le contre-exemple le plus petit est n=906 150 257 et il a été découvert par Minoru TANAKA en 1980.

Donc, la conjecture de Polya est fausse . Et pour conclure, une citation de Polya concernant l’enseignement des mathématiques :

A teacher of mathematics has a great opportunity. If he fills his allotted time with drilling his students in routine operations he kills their interest, hampers their intellectual development, and misuses his opportunity. But if he challenges the curiosity of his students by setting them problems proportionate to their knowledge, and helps them to solve their problems with stimulating questions, he may give them a taste for, and some means of, independent thinking.

² Mathematics is a vast, ever-growing, ever-changing subject. Among the innumerable questions that mathematicians ask, and mostly answer, some stand out from the rest : prominent peaks that tower over the lovely foothills. These are the really big questions, the difficult and challenging problems, that any mathematician would give his or her right arm to solve. Some remained unanswered for decades, some for centuries, a few for millennia. Some have yet to be conquered

Des preuves impliquant des calculs par ordinateur existent depuis un certain temps. La plus célèbre est la preuve du théorème des quatre couleurs. Le théorème des quatre couleurs indique qu’il est possible, en n’utilisant que quatre couleurs différentes, de colorier n’importe quelle carte découpée en régions connexes, de sorte que deux régions adjacentes, c’est-à-dire ayant toute une frontière (et non simplement un point) en commun reçoivent toujours deux couleurs distinctes.

Le résultat fut conjecturé en 1852 par Francis Guthrie, intéressé par la coloration de la carte des régions d’Angleterre. Deux premières démonstrations furent publiées, respectivement par Alfred Kempe en 1879 et Peter Guthrie Tait en 1880. Mais elles se révélèrent erronées ; les erreurs n’ont seulement été relevées qu’en 1890.

Si la preuve de Kempe s’est révélée fausse, elle fournit cependant une démonstration d’un problème analogue, avec cinq couleurs au lieu de quatre, aujourd’hui connu sous le nom du théorème des cinq couleurs.

En 1976, deux Américains, Kenneth Appel et Wolfgang Haken, affirment avoir démontré le théorème des quatre couleurs. Leur démonstration partage la communauté scientifique : pour la première fois une démonstration exige l’usage d’un ordinateur. Les deux mathématiciens avaient réussi à réduire l’infinité des possibles cartes à 1482 cartes exactement. Pour vérifier que ces 1482 cas de cartes, pourraient toutes être coloriées avec 4 couleurs seulement, ils ont écrit un programme informatique qui a testé les 1482 cas un par un (plus de 1200 heures de calcul). Depuis 1976, d’autres programmes informatiques, écrits de façon indépendante du premier, aboutissent au même résultat.

Jusqu’aujourd’hui aucune preuve qui puisse se passer de l’ordinateur n’a été découverte ; cependant, de nombreux amateurs continuent à être convaincus d’avoir démontré sans ordinateur le théorème des quatre couleurs. Dans le livre Mathematical Cranks (Underwood, 1992), tout un chapitre est dédié à ces tentatives parfois très drôles.

Comment savons-nous alors que la preuve du théorème des quatre couleurs est correcte ? Ces preuves par ordinateur sont-elles valables ? Pour la plupart des mathématiciens oui. La raison en est que, tant que nous vérifions le programme, le risque qu’un neutrino égaré transforme un 0 en 1 et produise un résultat erroné semble plus faible que le risque qu’il y ait une erreur dans l’une des centaines de pages de preuves faites à la main (comme celle du théorème de Fermat). Les êtres humains sont considérablement plus faillibles que les machines, si tant est que nous avons demandé à la machine de faire ce que nous voulions qu’elle fasse. Les preuves faites à la main ou chacun (qui dispose de connaissances mathématiques suffisantes) peut vérifier la preuve ligne par ligne restent bien-sûr préférables, mais ces preuves sont parfois difficiles à trouver. Dans ce cas une preuve par ordinateur est meilleure qu’aucune preuve (Hart, 2024).

Maintenant, avec les avancées récentes de l’intelligence artificielle, la question se pose si les ordinateurs seront bientôt capables de prouver des théorèmes tous seuls, sans aide d’un être humain. Selon la médaille Fields Terrence Tao on n’y est pas encore. Dans une interview avec Quanta Magazine, il déclare que les outils d’intelligence artificielle ne sont pas encore capables de faire des mathématiques de haut niveau de la recherche actuelle. Cependant, il est persuadé que cela viendra (Strogatz, 2024).

I think, the next cultural shift will be whether AI-generated proofs will be accepted. Right now, AI tools are not at the level where they can generate proofs to really advance mathematical problems. Maybe undergraduate-level homework assignments, they can kind of manage, but research mathematics, they’re not at that level yet. But at some point, we’re going to start seeing AI-assisted papers come out and there will be a debate. – Terrence Tao, 2024. 

Il existe aujourd’hui des projets visant à formaliser les preuves des grands théorèmes dans ce que l’on appelle des formal proof assistants. Ce sont des langages informatiques capables de vérifier à 100 % qu’un théorème est vrai ou non et donc qu’il est prouvé ou non (Strogatz, 2024). Ces assistants permettront des collaborations entre beaucoup plus de mathématiciens. Pour le moment, une collaboration sur un projet ne contient jamais plus de 5 mathématiciens. Dans une collaboration il faut soit faire 100 % confiance aux autres mathématiciens, soit vérifier tous leurs calculs et parties de preuves ligne par ligne. À plus de 5 personnes, ceci devient trop chaotique. Mais, une fois, que ces formal proof assistants sont mis en place, des collaborations bien plus grandes sont tout à fait possibles, car ces outils vérifieront les différentes étapes (Drösser, 2024).

Un exemple d’un tel assistant est donné dans le podcast Dernier Théorème de Fermat : à l’épreuve de l’informatique de la série La Science, CQFD de France Culture. Le podcast parle d’un assistant de preuve qui est en train de vérifier la preuve du Dernier Théorème de Fermat mentionné auparavant. Les 30 premières minutes du podcast font un joli résumé de l’histoire du Dernier Théorème de Fermat.

Références

1. Conrey, J.B. (2003). The Riemann Hypothesis. Notices of the American Mathematical Society. Volume 50. Number 3. https://www.ams.org/notices/200303/fea-conrey-web.pdf
2. Conway, J. H. and Sloane N. J. A. (1999) Sphere Packings, Lattices and Groups. Third edition. New York: Springer.
3. Drösser, C. (2024). AI Will Become Mathematicians’ ‘Co-Pilot’. Scientific American. June 2024. https://www.scientificamerican.com/article/ai-will-become-mathematicians-co-pilot/
4. Hart, S. (2024). A Mathematician’s View of Proof. Gresham College Lecture Series. https://www.gresham.ac.uk/watch-now/mathematician-proof
5. Klarreich, E. (2016). Sphere Packing Solved in Higher Dimensions. Quanta Magazine. https://www.quantamagazine.org/sphere-packing-solved-in-higher-dimensions-20160330/
6. Du Sautoy, M. (2003). The Music of the Primes. Harper.
7. Singh, S. (2002). Fermat’s Last Theorem. London: Fourth Estate.
8. Stewart, Ian. (2014). The Great Mathematical Problems : Marvels and Mysteries of Mathematics. London: Profile Books.
9. Strogatz, S. (2024). What makes for Good Mathematics? The Joy of Why. Quanta Magazine. https://www.quantamagazine.org/what-makes-for-good-mathematics-20240201/
10. Sullivan, B.W. (2013). Everything You Always Wanted To Know About Mathematics (But didn’t even know to ask). A Guided Journey Into the World of Abstract Mathematics and the Writing of Proofs. https://ia600408.us.archive.org/26/items/everything-you-always-wanted-to-know-about-mathematics/bws_book.pdf
11. Underwood, D. (1992). Mathematical Cranks. The Mathematical Association of America, Washington, 1992, v + 372.
12. Whitehead, A. N., and Russell, B. (1997). Principia Mathematica. Second edition. Cambridge: Cambridge University Press.