Dans ce module, nous allons jouer à un jeu appelé Involution©. Le jeu est composé d’un plateau et d’une manivelle. Le plateau contient 10 cavités qui contiennent chacune 1 anneau (d’une couleur).

Les anneaux peuvent être déplacés comme le montre la vidéo suivante :

Défi 1 

Mettez-vous en binômes et jouez à Involution© : essayez de résoudre les défis proposés sur les cartes.

Défi 2 

En partant de la configuration de gauche, est-il possible d’arriver à la configuration de droite ?

Si oui, expliquez vos mouvements. Sinon, pourquoi ?

Défi 3* 

Peut-on atteindre toutes les configurations d’anneaux ? Si oui, pourquoi ? Si non, lesquelles sont impossibles ? Justifiez votre réponse.

Pour y voir plus clair, essayons maintenant de jouer au même jeu, mais avec 9 anneaux blancs et un anneau noir.

La question essentielle est la suivante.

Défi 4* 

Est-il possible d’atteindre la configuration suivante à partir de n’importe quelle autre configuration ? Justifiez votre réponse.

Jouons maintenant avec deux anneaux noirs.

Défi 5* 

Est-il possible d’atteindre la configuration suivante à partir de n’importe quelle autre configuration ? Utilisez votre solution du défi 4 et justifiez votre réponse.

Jouons maintenant avec trois anneaux noirs.

Défi 6* 

Utilisez la solution du défi 5 pour déterminer si on peut atteindre la configuration suivante

à partir de n’importe quelle autre configuration.

Pour finir, jouons avec quatre anneaux noirs.

Défi 7* 

Utilisez la solution du défi 6 pour déterminer si on peut atteindre la configuration suivante

à partir de n’importe quelle autre configuration.

Défi 8* 

Reconsidérez le défi 3*.

Défi 9** 

Si nous jouons au même jeu, mais avec 12 anneaux (6 noirs et 6 blancs), est-il possible d’obtenir toutes les configurations ? Et avec 100 anneaux (50 noirs et 50 blancs) ?

Revenons au jeu avec 10 anneaux.

Défi 10 

En partant de la configuration suivante,

trouvez la configuration suivante

et comptez le nombre de mouvements.

Comparez vos solutions entre vous. Laquelle est la meilleure ? Définissez un critère pour évaluer quelle solution est meilleure qu’une autre.

Après discussion, essayez de compléter la définition suivante :

Une solution est optimale si

Nous allons maintenant construire une représentation visuelle de notre jeu afin de chercher une solution optimale. Rappelons-nous qu’au cours de Digital Sciences 1, un des premiers algorithmes que nous avions rencontrés était un algorithme pour retrouver un itinéraire avec le métro de New York. Tout comme le plan du métro qui est une représentation graphique du réseau réel, nous allons réaliser une représentation graphique du jeu : les nœuds du réseau sont les différentes configurations du jeu (dans le cas du métro, les nœuds étaient les stations) et deux configurations sont reliées par une ligne si on peut passer d’une configuration à l’autre par un mouvement (dans le cas du métro, deux stations sont reliées par une ligne si l’on peut aller d’une station directement à l’autre via le métro).

Prenons un exemple. Jouons à Involution©, mais avec seulement 5 anneaux et un plateau de jeu réduit (prenez le même plateau, mais sans utiliser les 5 cavités les plus à droite). Vous n’avez donc droit qu’à deux mouvements distincts de manivelle.

Défi 11 

La classe se divise en 3 groupes.

• Le premier groupe joue avec 1 anneau noir (et 4 anneaux blancs).
• Le deuxième groupe joue avec 2 anneaux noirs (et 3 anneaux blancs).
• Le troisième groupe joue avec 3 anneaux noirs (et 2 anneaux blancs).

Par groupe de deux, dessinez toutes les configurations possibles de votre version d’Involution©.

Discutez et expliquez ensemble combien de configurations de votre version d’Involution© sont possibles. Présentez ensuite votre solution et votre explication à l’ensemble de la classe.

Défi 12* 

Décidez si, dans votre cas, il est possible d’obtenir n’importe quelle configuration et expliquez votre réponse.

Nous allons maintenant construire la représentation graphique.

Défi 13 

Donnez un nom à chaque configuration (par exemple C₁, C₂, C₃, etc.). Pour chaque configuration trouvée dans le défi 11, dessinez un nœud et notez son nom à côté. Puis reliez deux nœuds par une ligne s’il est possible de passer d’une configuration à l’autre par un seul mouvement de manivelle. Comparez vos graphes.

Défi 14 

Reprenez le défi 12 (en utilisant le graphe que vous venez de construire).

Revenons maintenant au jeu initial avec 10 anneaux.

Défi 15* 

Savez-vous calculer le nombre de configurations différentes ou donner au moins une borne supérieure ?

En tout, il y a 252 configurations différentes. Ceci donne donc un graphe à 252 sommets, qui ressemble à ceci :

Le graphe d’Involution© avec 10 anneaux est beaucoup trop grand pour voir le chemin le plus court à l’œil nu. C’est pourquoi nous avons besoin d’un algorithme.

Défi 16 

Reprenez votre jeu et jouez maintenant avec 6 anneaux (3 noirs et 3 blancs) et un plateau de jeu réduit (prenez le même plateau, mais sans utiliser les 4 cavités les plus à droite). Trouvez toutes les configurations possibles et dessinez le graphe.

Défi 17 

Utilisez le graphe trouvé au défi 16 pour déterminer une solution optimale pour arriver à la configuration ci-dessous

en partant de la configuration suivante :

Défi 18 

En vous inspirant du défi précédent, cherchez un algorithme qui donne

1. le nombre minimal de mouvements pour aller d’une configuration à une autre (une fois que le graphe du jeu est donné).
   
   Aide
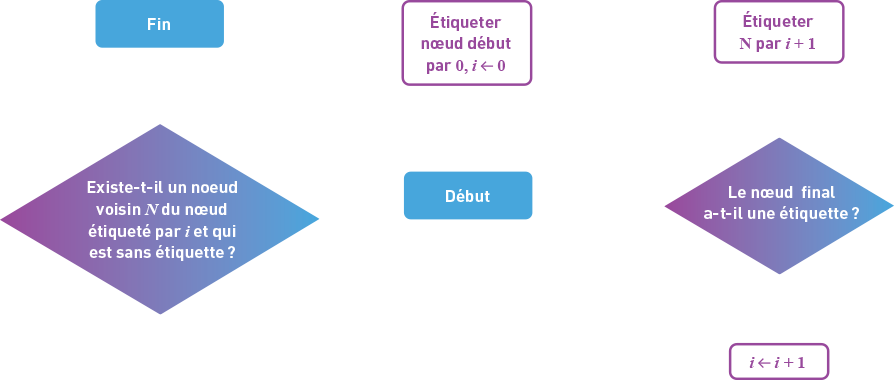
2. une solution optimale pour aller d’une configuration à une autre (une fois que le graphe du jeu est donné).
   
   Aide

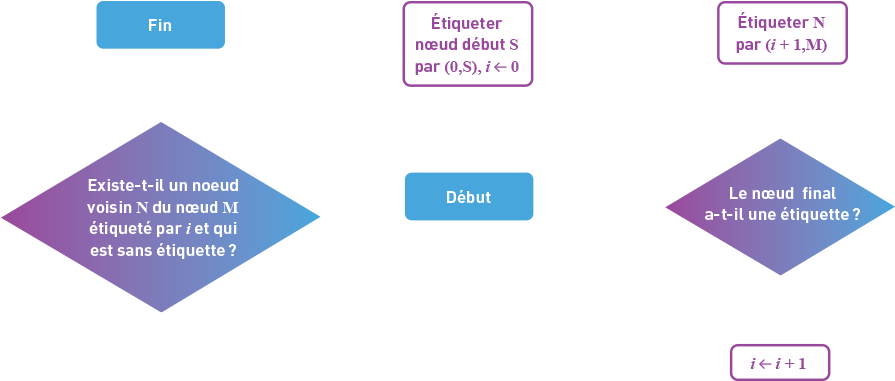
Inscrivez les instructions informelles de votre algorithme et dessinez son organigramme de programmation.

Défi 19

Généralisez l’algorithme au jeu Involution© avec 10 anneaux.

Défi 20

Regardez l’image suivante :

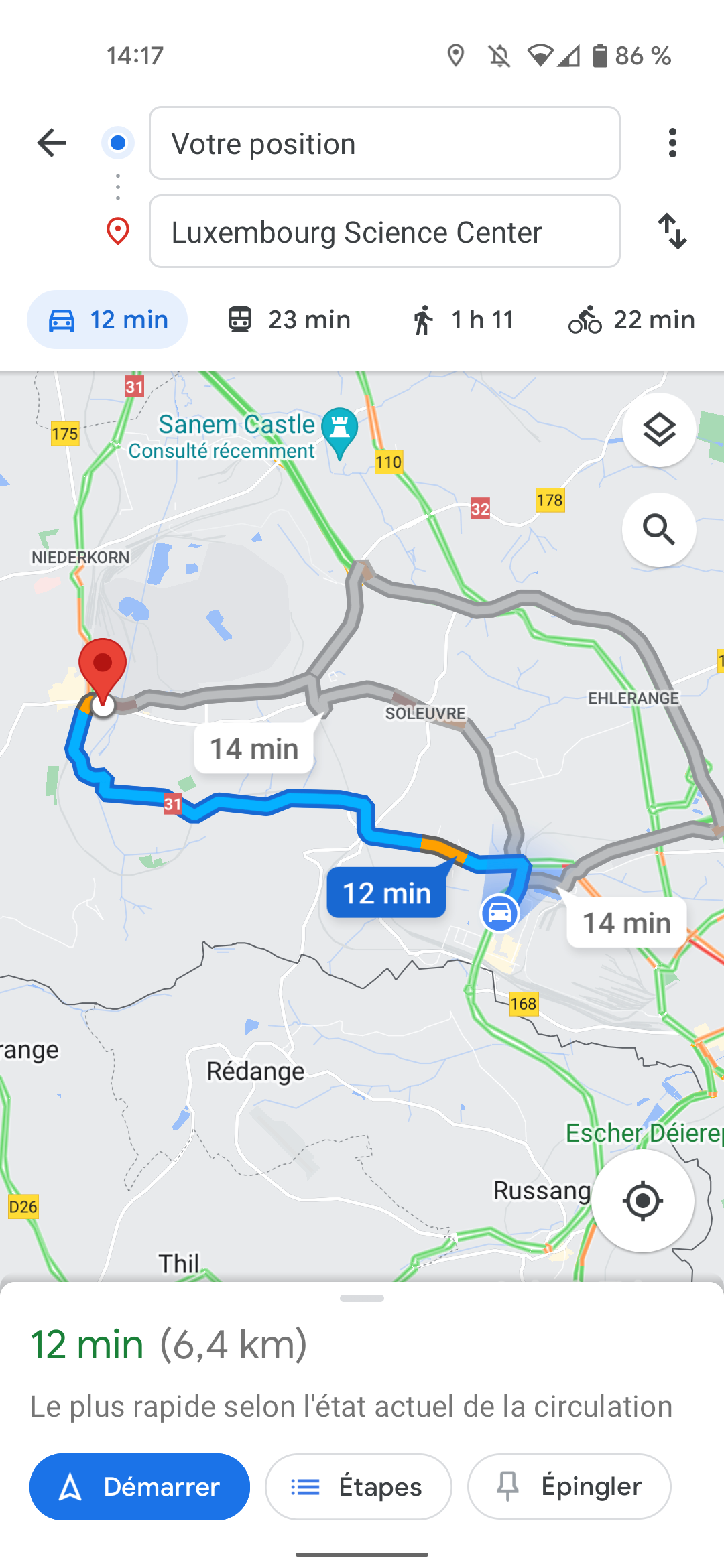
De quelle application s’agit-il? Cherchez un lien entre cette application et la recherche d’une solution optimale dans le jeu Involution©.