Das Spiel kann im Centre de documentation pédagogique des IFEN oder im F.use (Future Space for Education) auf dem Campus Belval ausgeliehen werden.
1.2 Unterrichtsplanung
Da die Module unabhängig voneinander funktionieren, kann dieses Modul im Unterricht behandelt werden, ohne dass die anderen Module behandelt werden müssen.
Dieses Modul wurde in Zusammenarbeit mit Hugo Parlier und Bruno Teheux vom Mathematischen Department der Universität Luxemburg ausgearbeitet.
02
Bedingungsanalyse
- Zielgruppe: 7e-5e klassischer und allgemeiner Sekundarunterricht
- Raum: Es sind keine besonderen Räumlichkeiten vorzusehen
- Benötigtes Material:
- Das Spiel Involution©: Das Spiel kann im Centre de documentation pédagogique des IFEN oder im F.use (Future Space for Education) auf dem Campus Belval ausgeliehen werden.
- Computer oder Tablets können verwendet werden, um die Anweisungen zu lesen, notwendig ist das aber nicht. Die Anweisungen können auch einfach ausgedruckt werden.
- Dauer: 2 Unterrichtsstunden
03
Sachanalyse
Die Hauptidee dieser Stunde besteht darin, das im Unterricht behandelte Thema „Algorithmen“ zu konkretisieren, und zwar mit Involution©, einem Spiel, das von Hugo Parlier und Bruno Teheux, zwei Mathematikwissenschaftlern der Universität Luxemburg, entwickelt wurde. Durch dieses Spiel werden die Schüler*innen auf spielerische Weise mit mathematischen und algorithmischen Konzepten wie dem Algorithmus des kürzesten Pfads sowie optimalen und nicht-optimalen Strategien vertraut gemacht. Das Spiel besteht aus einer Anordnung von 10 schwarzen und weißen Ringen. Eine kreisförmige Kurbel wird auf das Spielbrett gesetzt und durch eine Kurbelbewegung werden die Positionen der Ringe verändert. Ziel des Spiels ist es, die Position der Ringe so zu verändern, dass man ausgehend von einer Startkonfiguration zu einer bestimmten Zielkonfiguration gelangt.
04
Didaktische Analyse
a. Angestrebte Lernziele und Kompetenzen
b. Didaktische Relevanz und Begründung
c. Didaktische Reduktion
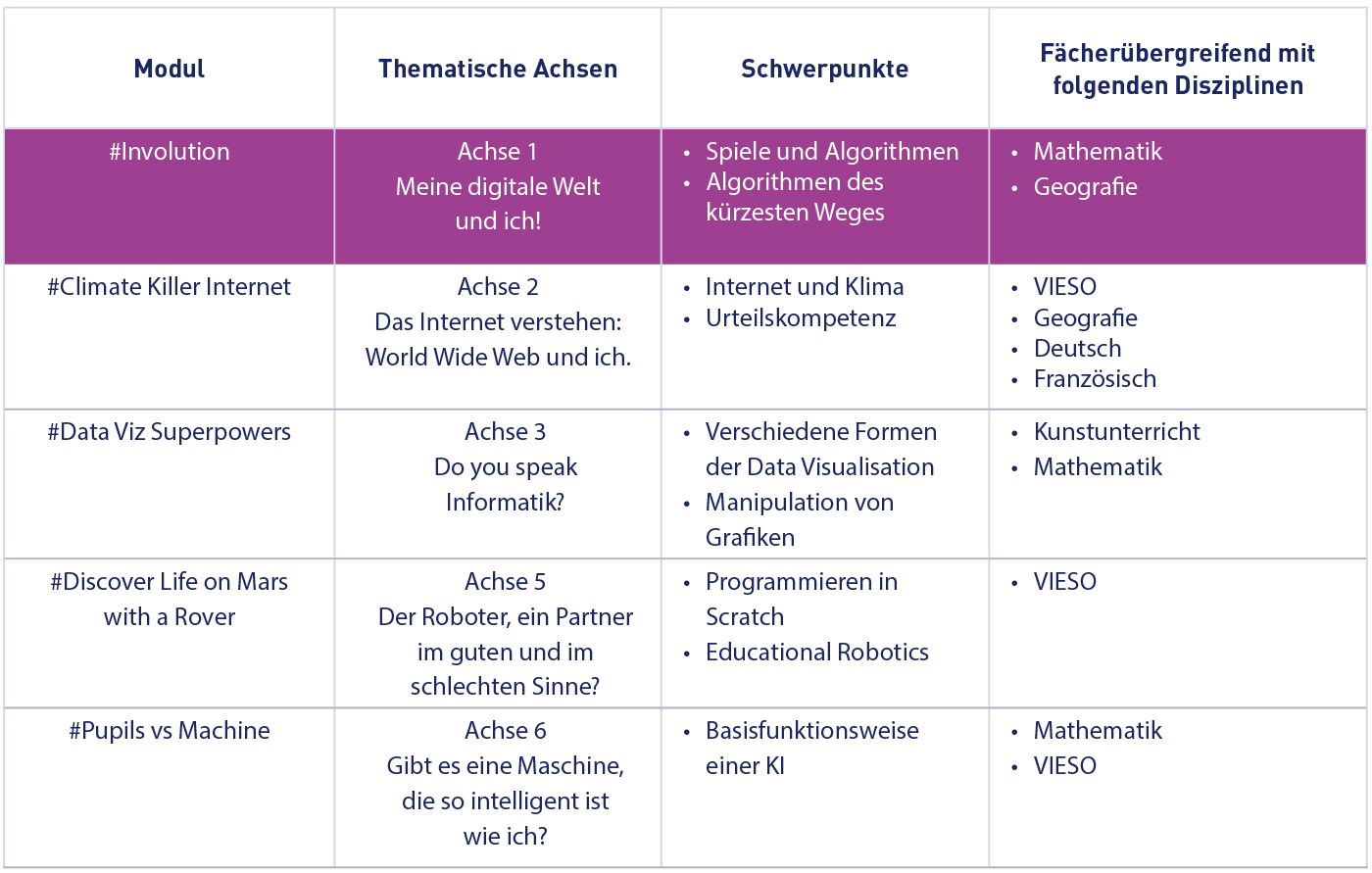
Angestrebte Kompetenzen der Achse 1: Meine digitale Welt und ich!
- WISSEN: Grundkenntnisse des allgemeinen digitalen und computerbezogenen Vokabulars, der Kommunikation zwischen Mensch und Computer (Algorithmus) und des Abstraktionsprinzips bei der Problemlösung.
- FACHKOMPETENZ: Zerlegung eines Problems zum Zweck der Problemlösung, Konzeption und Darstellung eines Algorithmus, Entwicklung und Anwendung eines einfachen Algorithmus mit Karten und einem Programmablauf.
- VERHALTEN: Förderung des Bewusstseins für die Bedeutung der Informatik für die täglichen Aufgaben auf der Grundlage der gewählten Tools, der bereitgestellten Informationen und der erzielten Ergebnisse.
Lernziele aus dem Medienkompass1
- MK2 – Kommunikation und Zusammenarbeit: 2.1 Mit anderen zusammenarbeiten
- MK3 – Erstellen von Inhalten: 3.3 Modellieren, strukturieren und codieren
In diesem Modul sollen das Konzept und die Funktionsweise von Algorithmen anhand eines Spiels verständlich gemacht werden. Eine Besonderheit des Moduls ist, dass keine elektronischen Technologien, weder Computer noch Tablets, verwendet werden. Mit solchen „Unplugged“-Aktivitäten sollen Schüler*innen in die Welt der Informatik eingeführt werden, um „die technologische Komplexität beim Lernen zu beseitigen und die Grundbegriffe der Informatik zu vermitteln“ (INRIA, 2020). Der Zugang wird dadurch erleichtert und verdeutlicht einen wesentlichen Aspekt der digitalen Arbeit: Digitale Kulturen haben in erster Linie nichts mit Computern im Sinne von elektrischen Maschinen zu tun – das Merkmal der Algorithmizität beispielsweise, das im Mittelpunkt dieses Moduls steht, lässt sich durch die Bildung formaler mathematischer und logischer Modelle beschreiben, die auch mechanisch dargestellt werden können. Um den Informatiker Leslie Lamport zu zitieren: „Die Bedeutung des Nachdenkens und des Aufschreibens vor dem Codieren sollte bereits in der Vorschule gelehrt werden, wird es aber nicht.“ (Han, 2022).
So knüpft das Modul #Involution an die in der Grundschule vermittelten Grundlagen des Codierens an und entwickelt sie an der Schnittstelle von Mathematik und Informatik weiter.
Involution© bietet mehrere Challenges mit unterschiedlichem Schwierigkeitsgrad aus dem Bereich der „Shortest Path“-Problematik und stellt sie in den Rahmen des kooperativen und problemlösenden Lernens . Das Spiel regt einen gezielten kognitiven Prozess an, der anhand des verteilten Unterrichtsmaterials aktiv entwickelt werden kann. Bei der Planung und Durchführung der Unterrichtseinheit kann zugunsten eines freien Experimentierens mit Involution© und den zur Verfügung gestellten Anweisungen auf eine strikte Zeiteinteilung völlig verzichtet werden. Die Festigung von Wissen und Kompetenzen erfolgt durch das Lernen im Unterricht, indem die Schüler*innen der Klasse ihre Lösungen sowie die Gründe für ihre Entscheidung präsentieren.
05
Methodische Analyse
In diesem Modul spielen die Schüler*innen ein Spiel namens Involution©. Die Aufgabe besteht darin, durch Drehen der Kurbel von der oberen zur unteren Konfiguration zu wechseln.

Eine kreisförmige Kurbel wird auf das Spielbrett gesetzt und durch eine Kurbelbewegung werden die Positionen der Ringe verändert. Ziel des Spiels ist es, die Position der Ringe so zu verändern, dass man ausgehend von einer Startkonfiguration zu einer bestimmten Zielkonfiguration gelangt.
Das Spiel
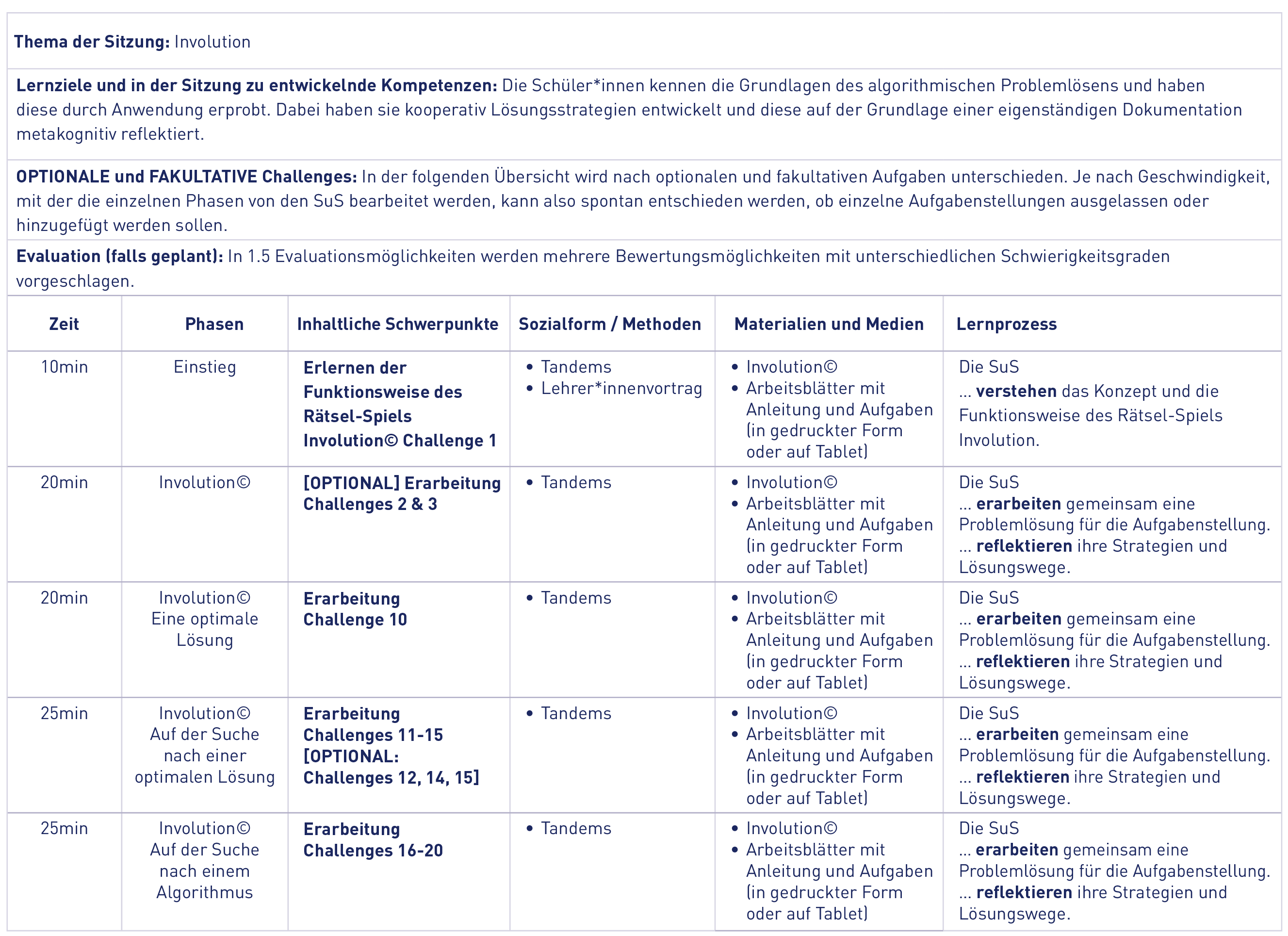
Die Lehrkraft erklärt kurz das Prinzip des Spiels. Der Einstieg in die Thematik erfolgt über das Spiel selbst. Die Schüler*innen bilden Zweiergruppen. Jede Gruppe erhält eine Box, die ein Spielbrett (zum Zusammenbauen) und Aufgabenkarten enthält. Auf jeder Karte sind zwei Konfigurationen abgebildet. Die Aufgabe besteht darin, durch Drehen der Kurbel von der oberen zur unteren Konfiguration zu wechseln. Die Schüler*innen beginnen, die Aufgaben in der vorgegebenen Reihenfolge zu lösen. Diese Aktivität ist die erste von vielen Challenges in diesem Modul. Alle Challenges sind in den Materialien beschrieben.
Nach diesem Einstieg in die Thematik gehen die Schüler*innen zu den verschiedenen Challenges über. Im besten Fall werden alle Challenges gelöst. Solche Challenges, die mit einem Sternchen gekennzeichnet sind, sind schwieriger (und mathematischer). Sie sind für motivierte Schüler*innen gedacht. Es gibt auch optionale Challenges (wie im Stundenverlaufsplan (siehe unten) angegeben), das Modul funktioniert jedoch auch ohne diese Challenges.
Challenge 2: Nach der ersten Phase, sobald die Schüler*innen das Prinzip des Spiels verstanden haben, gehen sie zu Challenge 2 über. Die Lehrkraft teilt die Klasse in drei Gruppen auf; eine Gruppe bearbeitet die erste Unterchallenge, die andere die zweite und die andere die dritte. Hinweis: Die erste Challenge ist etwas einfacher als die beiden anderen. Dies ist bei der Gruppenaufteilung und der Verteilung der Challenges zu berücksichtigen.
Sobald die Challenge gelöst ist, müssen sich die Schüler*innen in ihrer Gruppe abstimmen und dann ihr Ergebnis dem Rest der Klasse mitteilen.
Challenge 3*: Die Challenge 3 ist schwieriger und optional. Sie ist für leistungsstarke und motivierte Schüler*innen gedacht.
Wie gelangt man zu allen Konfigurationen?
Dieser Abschnitt hilft den Schüler*innen bei der Lösung von Challenge 3. Er richtet sich daher nur an diejenigen Schüler*innen, die sich mit der Challenge 3 beschäftigt haben. Von den in diesem Abschnitt vorgestellten Challenges ist die Challenge 9 besonders schwer. Wir überlassen es der Lehrkraft zu entscheiden, welche Schüler*innen diesen Teil mit oder ohne Challenge 9 bearbeiten können/sollen.
Dieser Abschnitt führt die Schüler*innen über das mathematische Prinzip der Induktion zu einer Lösung von Challenge 3 (ohne dieses Prinzip explizit zu erwähnen oder auszuführen).
Eine optimale Lösung
Challenge 10: Bei Challenge 10 suchen die Schüler*innen nach einer Lösung und zählen die Anzahl der Kurbelbewegungen bis zur Lösung. Sie vergleichen ihre Lösungen untereinander.
In einer moderierten Diskussion kommen die Schüler*innen zu dem Schluss, dass eine Lösung besser ist als eine andere, wenn sie weniger Kurbelbewegungen erfordert.
Im Klassenplenum wird gemeinsam eine Definition ähnlich wie die folgende erarbeitet:
Eine Lösung ist optimal, wenn sie mit möglichst wenigen Kurbelbewegungen gefunden wird.
Auf der Suche nach einer optimalen Lösung
Wie findet man eine solche optimale Lösung? Kontextualisieren Sie diese Frage mit der Suche nach einer möglichst kurzen Strecke im New-Yorker U-Bahn-Netz, die im Kurs Digital Sciences 1 behandelt wird.
Wie kann man das Spiel in Form eines Graphen darstellen?
Dieser Abschnitt beginnt mit einem ganz einfachen Beispiel: das Spiel Involution© wird vorgegeben, aber mit nur fünf Ringen und einem verkleinerten Spielbrett. Die fünf Vertiefungen ganz rechts dürfen nicht benutzt werden. Es gibt also nur zwei mögliche Positionen, an denen die Kurbel angesetzt werden kann.
Challenge 11: Die Lehrkraft teilt die Klasse in drei Gruppen ein. Innerhalb der Gruppen spielen die Schüler*innen das Spiel weiter in Zweiergruppen.
- Die erste Gruppe spielt mit 1 schwarzen Ring (und 4 weißen Ringen).
- Die zweite Gruppe spielt mit 2 schwarzen Ringen (und 3 weißen Ringen).
- Die dritte Gruppe spielt mit 3 schwarzen Ringen (und 2 weißen Ringen).
Die Schüler*innen lösen ihre jeweilige Aufgabe in Zweiergruppen. Anschließend stimmen sie sich in ihrer Gruppe ab und teilen ihr Ergebnis dem Rest der Klasse mit.
Challenge 12*: Diese Challenge ist schwieriger und optional.
Die Schüler*innen gehen dazu über, das Spiel grafisch darzustellen (mit dem verkleinerten Spielbrett).
Challenge 13: Für dieses, sowie auch die folgenden Challenges, muss das Konzept von Graphen eingeführt, respektiv kurz wiederholt werden. Die Schüler*innen arbeiten in Zweiergruppen. Anschließend vergleichen sie ihr Ergebnis. Sie werden feststellen, dass der zweite Fall und der dritte Fall genau gleich sind. In einer moderierten Diskussion werden die Schüler*innen zu der Erkenntnis hingeführt, dass diese beiden Fälle symmetrisch sind.
Challenge 14: Sobald der Graph erstellt ist, wird die Challenge 12 viel einfacher. An den Graphen können die Schüler*innen die Antwort deutlich ablesen.
In der nächsten Phase gehen die Schüler*innen wieder zum Spiel mit 10 Ringen über (5 schwarze und 5 weiße Ringe).
Challenge 15*: Diese Challenge ist optional. Sie soll den Schüler*innen vor Augen führen, dass das Zählen umso komplizierter wird, je komplexer das Problem ist. Viele Schüler*innen sind sich dessen nicht bewusst, da das Zählen bei wenigen Objekten sehr einfach ist.
Die grafische Darstellung des Spiels Involution© ist gegeben, aber sie ist zu groß, um mit bloßem Auge den kürzesten Pfad zu finden.
Auf der Suche nach einem Algorithmus
Um die Suche nach einem Algorithmus zu erleichtern, gehen die Schüler*innen zu 6 Ringen über (3 schwarze und 3 weiße). Der Graph bei Involution© mit 6 Ringen ist klein genug, um manuell den kürzesten Pfad zu finden (im Gegensatz zum Graph bei Involution© mit 10 Ringen), aber groß genug, damit die Lösung nicht zu leicht ist (im Gegensatz zu Involution© mit 5 Ringen).
Challenge 16 und 17: Diese Challenges dienen dazu, die Schüler*innen an einen Algorithmus heranzuführen. Sie werden in Zweiergruppen bearbeitet. Die Ergebnisse werden dann in der Klasse in Form einer moderierten Diskussion besprochen.
Challenge 18: Bei dieser Challenge wird der Algorithmus manuell erstellt. Die Schüler*innen sollen informelle Anweisungen verfassen. Punkt b) ist komplexer. Er ist nur für motivierte Schüler*innen gedacht.
Beim Zeichnen des Ablaufdiagramms können die Schüler*innen entweder alles selbst zeichnen oder die Arbeitshilfe verwenden, in der die Felder bereits vorgegeben sind. Anschließend sollen die Schüler*innen die Felder in die richtige Reihenfolge bringen und die Pfeile hinzufügen, um ein Ablaufdiagramm zu gestalten.
Challenge 19: Diese Challenge dient nur dazu, den Schüler*innen vor Augen zu führen, dass der allgemeine Algorithmus genau der ist, den sie gerade erstellt haben. Diese Challenge sollte direkt in einer moderierten Diskussion bearbeitet werden.
Challenge 20: In der moderierten Diskussion sollen die Schüler*innen erkennen, dass der Algorithmus, den sie gerade erstellt haben, ein Algorithmus des kürzesten Pfads darstellt. Diese Arten von Algorithmen werden auch von GPS-Navigationssystemen verwendet (siehe 1.6.02 Die Bedeutung von Graphen in den Digitalwissenschaften).
06
Differenzierungsmöglichkeiten
Für Anfänger
Das Modul ist durchaus machbar, wenn man die Challenges und den Abschnitt weglässt, die mit einem Sternchen markiert sind. Ermutigen Sie schwache Schüler*innen, das Modul ohne diese Challenges zu absolvieren.
Für besonders motivierte Schüler*innen
Beziehen Sie bei besonders motivierten Schüler*innen die mit einem Sternchen versehenen Challenges (und den mit einem Sternchen markierten Abschnitt) mit ein. Diese Challenges sind mathematischer und erfordern logisches Denken. Es gibt eine Challenge, die mit zwei Sternchen gekennzeichnet ist. Diese ist nur für sehr leistungsstarke Schüler*innen geeignet, die mit dem Thema gut zurechtkommen.
Bei den Challenges 2 und 11 kann die Lehrkraft die drei Gruppen so bilden, dass die Gruppe, die den etwas einfacheren Fall bearbeitet, aus leistungsschwächeren Schüler*innen besteht.
Die Challenge 18, die Haupt-Challenge, bei der der Algorithmus erstellt wird, hat drei Schwierigkeitsstufen:
- Erstellung eines Algorithmus, der nur die geringstmögliche Anzahl von Kurbelbewegungen zählt und/oder bei dem die Felder des Ablaufdiagramms bereits vorgegeben sind.
- Dasselbe ohne die Felder des Ablaufdiagramms
- Erstellung eines Algorithmus, der die geringstmögliche Anzahl von Kurbelbewegungen und die Folge der Bewegungen zählt
07
Weitere im Rahmen der Unterrichtsreihe zu erfüllende Qualitätskriterien
- Luxemburgischer Kontext: Das Spiel Involution© wurde von Hugo Parlier und Bruno Teheux, zwei Mathematikwissenschaftlern der Universität Luxemburg, entwickelt. In seiner aktuellen Form kann es an die Inhalte des luxemburgischen Medienkompasses anknüpfen und entspricht der Themenachse I des Fachs Digital Sciences.
- Differenzierung: In diesem Modul sind einige Challenges optional. Die mit einem Sternchen markierten Challenges sind schwieriger als die anderen und können je nach Niveau der Klasse und/oder der Schüler*innen bearbeitet oder weggelassen werden.
- Medienkompass: Vgl. die angestrebten Lernziele des Medienkompetenzrahmens innerhalb der didaktischen Analyse des vorliegenden Dokuments.
- 4K-Modell: Kommunikation, Kollaboration, Kreativität, kritisches Denken:
Das 4K-Modell wird durch die verschiedenen Sozialformen und Unterrichtsaktivitäten auf unterschiedliche Weise aufgegriffen. - Bezug zur aktuellen Forschung: Die Challenges von Involution© gehören zur Familie der Rekonfigurationsproblematik (Combinatorial reconfiguration), einem aktuellen Forschungsgebiet, das in der Mathematik und Informatik untersucht wird. Die Algorithmen des kürzesten Pfads sind zwar schon über 50 Jahre alt, aber immer noch ein aktives Thema in der Forschung, um Anwendungen für die Suche nach dem kürzesten Pfad zu optimieren.
- Bezug zur Forschung in Luxemburg: Das Spiel Involution© wurde von zwei Wissenschaftlern der Universität Luxemburg entwickelt. In dem Podcast in 1.7 Wissenschaftler*innen kommen zu Wort erklärt Hugo Parlier, wie er Spiele entwickelt, in die die Ergebnisse seiner Forschung einfließen.
Referenzen
Institut national de recherche en sciences et technologies du numérique (INRIA). (2020). Éducation et Numérique : enjeux et défis. Livre Blanc N 04. https://hal.inria.fr/hal-03051329v2/document
Han, Sheon. (2022). How to Write Software With Mathematical Perfection. Quantamagazine. https://www.quantamagazine.org/computing-expert-says-programmers-need-more-math-20220517