1.2 Lesson planning
- Target audience : 6e
- Place : a typical classroom
- Materials required : at least one computer or tablet with internet access per group of 2 pupils.
- Duration : 2 or 3 times 90 minutes
Skills targeted by the mathematics course
- Use an algebraic expression to model situations and describe dependencies.
- Describe a series of figures or a series of numbers using an algebraic expression.
- Use a calculator or software to calculate a numerical value.
- Decode an algebraic expression into an ordered series of calculation instructions and formalise the algorithm.
Skills targeted by the natural sciences course (Naturwissenschaften)
- Formulate well-founded hypotheses based on the context, using examples.
- Make targeted observations, present and evaluate the results, and draw conclusions.
- Recognise simple cause-and-effect relationships and draw logical conclusions.
- Diagrammatic representation and interpretation of the models presented.
Competences covered by the Reference Guide for Media Literacy1
- Competences 1 : 1.2 Analysing and assessing data, information and digital content.
- Compéeences 2 : 2.1 Working with others 2.3 Using appropriate forms of expression (netiquette).
- Competences 3 : 3.3 Modelling, structuring and coding
1https://edumedia.lu/wp-content/uploads/2024/12/Medienkompass_EN_web.pdf
In this module, students are required to immerse themselves in mathematical conjectures. They must first explore examples, then establish a conjecture, try to prove it and finally formulate a theorem. The various conjectures are available in a blanc version (M1) (without help or hints) and a guided version (M2) (with help, hints and gap-fill texts).
Before the lesson : the teacher divides the pupils into groups of 4. As the problems have different levels of difficulty, it is preferable to group the pupils according to level. The teacher will then decide in advance which group will work on which conjectures.
Note that conjectures 7 and 8 are very difficult. They are supposed to be given to groups of students who are very strong in mathematics. The teacher should also bear in mind that it is not at all necessary to work on every conjecture in this module. If necessary, several groups can also work on the same conjecture.
There are 15 conjectures in all. The conjectures are of different types:
- Conjectures 1 to 8 : these are true theorems that are easy to prove and have short proofs. However, they have different levels of difficulty (see table below)
- Conjectures 9 to 12 : these are refuted conjectures, i.e. they can be proved false, or a counterexample can be found. These statements are made in such a way that if we restrict ourselves to testing the first 5 cases, these statements appear to be true. However, by testing a larger number of cases (n=40 for 9, the 8thexample for 10, n=5 for 11 and n=15 for 12), we quickly come across a counterexample that refutes the conjecture.
- Conjectures 13 to 15 : These are open conjectures, which mathematicians are convinced are true, but no one has yet been able to prove them. Of course, students are not expected to prove these open conjectures. The idea is to familiarise them for the first time with the concept of an open mathematical conjecture. The conjectures chosen are all easy to understand and the examples illustrating them are feasible for students in secondary school.
The following table summarises the nature and level of difficulty of the various conjectures.
| Nature of the conjecture | easy | Medium | Difficult | very difficult |
| True theorem | 01, 02 | 03, 04, 06 | 05 | 07, 08 |
| Refuted conjecture | 09, 12 | 10 | 11 | / |
| Open conjecture | / | 14 | 13, 15 | / |
The unit can be done in two or three stages. In the case of two stages, true and provable statements (conjectures 1 to 8) are dealt with during stage 1. In the next stage, open and disprovable statements (conjectures 9 to 15) are dealt with. In other case, step 1 deals with true and provable statements (conjectures 1 to 8), step 2 with disproved statements (conjectures 9 to 12) and the final step with open statements (13 to 15).
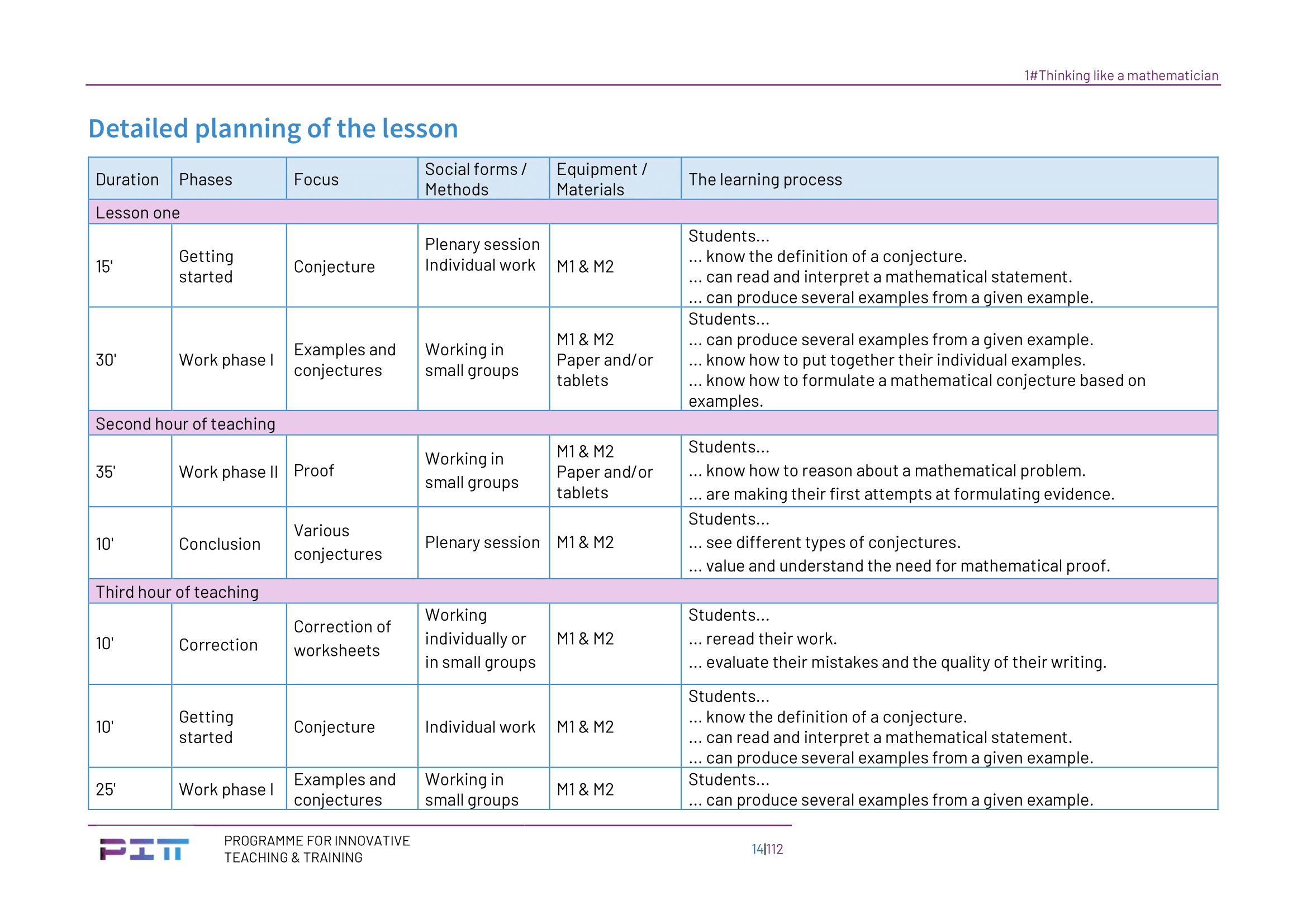
First hour of teaching
Introduction (15 min): The teacher gives a short introduction to the concept of conjectures. The following definitions can be given (or any other definition of conjecture).
Definition 1. A conjecture is an assertion for which a proof is not yet known, but which is strongly believed to be true.
Definition 2. A conjecture is a hypothesis that has not yet been confirmed.
Definition 3. A conjecture is a proposition that is made on the basis of observations, apparent patterns, or numerical results, but which has not yet been formally proven. Mathematicians formulate conjectures when they notice regularities in the data or patterns in their research.1
The conjectures are distributed to the students under the form of the blanc version and they work individually for the moment. The teacher tells each pupil which conjecture (from conjectures 1 to 8) to work on (according to the distribution established earlier) and lets them work individually.
Examples and conjectures (30 min): The pupils get into groups, the groups being designated by the teacher. They think about examples, a conjecture and an idea for a proof. The teacher moves around the classroom to help and answer questions, if necessary.
Second hour of teaching
Formulation of evidence (35 min): The pupils try to formulate a proof, or an explanation for the phenomenon observed. They think about how to formulate their conclusion.
Important notes :
- Students may use any language to discuss in their group. However, the written material must be produced in French. This is important so that, on the one hand, the students practise mathematical writing in French and, on the other hand, by writing in French, the students remain consistent with the language of the course and the vocabulary learned in class.
- In this module, it is important that students dare to think about mathematical problems. Their writing does not have to be perfect. The teacher should encourage them to try to describe their ideas, even if their writing is not mathematically neat and rigorous. The slogan Promote imperfection to ultimately demand perfection
- This first part can be done without the use of ICT (Information and Communication Technologies). However, we recommend that teachers allow students to at least use calculators or spreadsheets. For teachers who want to incorporate more technology, other tools may prove useful.
Conclusion (10min): Each group will briefly present its conjecture. A group discussion will follow on the complexity of the problem and the key stages (finding examples, formulating a conjecture, finding a proof, formulating a theorem).
End of lesson: The teacher will collect all the completed worksheets and correct them for the next time.
Differentiation: The different conjectures are available in a blanc version (M1) (without help or clues) and a guided version (M2) (with help, clues and fill-in-the-blanks). When a group of pupils seems to be struggling, the teacher can give them the guided version of the problem. The distribution of the guided version will be adapted to the specific needs of each group, depending on their progress and particular difficulties.
Note that the lesson plan is based on the time needed when the students are working on the blanc version of the conjectures. If the whole class works on the guided version from the start, the time needed can be halved.
Third hour of teaching
Distribution of corrected worksheets (10 min): The corrected worksheets of the previous lesson are handed out to the students. The students look through them and can ask questions.
Introduction (10 min): The teacher tells each student which conjecture to work on (among conjectures 9 to 15 if the module is done in two stages only, otherwise among conjectures 9 to 12 and according to the distribution established earlier) and lets them work individually. If the module is done in two stages only, the teacher ensures that at least one conjecture from each category (open statements and disproved statements) is worked on.
Examples and conjectures (25 min): The pupils get into groups; the groups being designated by the teacher. They think about examples, a conjecture and an idea for a proof. The teacher circulates around the class to help and answer questions, if necessary.
Fourth hour of teaching
Formulating evidence (35 min): The pupils try to formulate a proof, or an explanation for the phenomenon observed. They think about how to formulate their conclusion.
Important information:
- Students may use any language to discuss in their group. However, the written material must be produced in French. This is important so that, on the one hand, the students practise mathematical writing in French and, on the other hand, by writing in French, the students remain consistent with the language of the course and the vocabulary learned in class.
- In this module, it is important that students dare to think about mathematical problems. Their writing does not have to be perfect. The teacher should encourage them to try to describe their ideas, even if their writing is not mathematically neat and rigorous.
- For this second part we recommend the use of ICT (Information and Communication Technologies). Spreadsheets (e.g. Excel) or computer programs (e.g. WolframAlpha, Scratch etc.) are very useful. Without them, counterexamples to statements 9 to 12 are hard to find. For open conjectures, it is necessary to let the students search the Internet or ask an artificial intelligence (e.g. ChatGPT, ShulKI etc.) for help. They could be left to fend for themselves without any research tools at first and only use the Internet later. The fact of thinking about the problem first and only later finding, via a search tool, that the statement is in fact an open conjecture, will increase the pupils’ astonishment.
Conclusion (10 min): Each group briefly presents its conjecture. A group discussion follows on the complexity of the problem and the key stages (finding examples, formulating a conjecture, finding a counterexample or discovering that it is an open problem, formulating a conclusion). The concepts of counterexample and open problem are discussed.
End of lesson: The teacher will collect all the copies and mark them for the next time.
Differentiation: The different conjectures are available in a blanc version (without help or clues) and a guided version (with help, clues and gap-fill texts). When a group of pupils seems to be struggling, the teacher can give them the guided version of the problem. The distribution of the guided version will be adapted to the specific needs of each group, depending on their progress and particular difficulties.
Note that the lesson plan is based on the time needed when the students are working on the blanc version of the conjectures. If the whole class works on the guided version from the start, the time needed can be halved.
Fifth and sixth teaching hours (optional)
These two hours of teaching are optional. If these lessons are done, statements 9 to 12 are dealt with in the third and fourth lessons and statements 13 to 15 in the following two lessons. The same lesson plan applies as before.
Seventh (resp. Fifth) lesson: Closure
Distribution of corrected worksheets (10 min): The corrected worksheets of the previous lesson are handed out to the students. The students look through them and can ask questions.
As described in the previous paragraph, the closure can be done after the fourth or sixth lesson. This lesson takes place according to the concept of pedagogical walls (murs pédagogiques, Agostino & de Versailles, 2024). Since it was set up at the start of the 2017 academic year at the Lycée de la Plaine de Neauphle in Trappes in the Yvelines, the pedagogical device described in this chapter, which we call “Pedagogical Walls”, can now be found in the classroom practices of several teachers. The name comes from the fact that some classrooms are equipped with whiteboards mounted on the walls. The boards are positioned all along the free walls and make it possible to create mini-classes by organising the students’ tables in a horseshoe shape around each board.
Set-up (5 min): At the start of the session, the pupils are divided into groups of four to six. Each group sits facing one of the boards or simply around a table, as the boards are not essential. It is important to mix the groups and not to keep the same groups as in the previous phases.
Important note: If the second and third lessons have been done in one lesson, the teacher must ensure that each group has at least one student who has previously dealt with a false conjecture and one student who has dealt with an open conjecture.
First phase (18 min). The fake Instagram publications (M3) are distributed among the different groups. There must be at least two different publications for the second phase of the scenario to be possible. Each group can use the board to share and test their attempts. If boards are not available, students can simply write on sheets of paper or tablets. No write-up is expected. Indeed, it might be tempting to ask the students to write down a solution in their own notebooks in a bid to maximise everyone’s work, but this is not in line with the main aim of the activity, which is to reach a solution by sharing ideas orally with written support on the board. In this activity, the aim of the written work is to enable the pupils to retain ideas or carry out calculations. (Agostino & de Versailles, 2024). The aim is for pupils to read and discuss the Instagram posts (M3) and comments:
- Who’s right?
- Who’s wrong?
- Why is this?
To defend their ideas, they must use the conjectures they have seen in previous lessons (e.g. “the assertion is false because we also saw a conjecture that seemed to work but no longer worked from n=40”).
Note: Not all Instagram publications have the same level of difficulty. Here is a table summarising the publications and their difficulty.
| Publication | Features | Level of difficulty |
| 1 |
|
Easy |
| 2 |
|
Medium |
| 3 |
|
easy |
| 4 |
|
medium |
| 5 |
|
Difficult |
| 6 |
|
Difficult |
Second phase (7 min): At the end of the first phase, the groups change mini-classes. One pupil per group stays in their place (chosen by consensus or by the teacher) to present the Instagram publication studied previously to the new group, using the publication and the notes on the board as a basis. The newcomers take notes, ask questions or correct if necessary. This is also an opportunity to finish unfinished work. Note-taking is permitted because it encourages concentration and reproduces the usual attitude in class. This phase allows the learners to quickly reinvest what they have learned in the first stage.
Because of the change of groups, it is essential to distribute at least 2 different Instagram publications to the groups. You don’t want a student who moves to find the same Instagram publication as the one they’ve already studied.
Phase 2 takes less time. The explanation by the remaining pupil is generally correct (the fruit of the previous collective reflection), and the essential part consists of understanding and answering the group’s questions. This process is naturally quicker than the initial development of the solution.
Closing (5 min): The session can end with a collective moment where each group briefly answers a question such as “What have you learnt today?” or “What have you gained from this session?”. This period clearly marks a return to the collective, with the pupils expressing themselves for the first time in front of the whole class and the teacher. This activity enables the teacher to check that the pupils have acquired the vocabulary they need and to assess their ability to articulate logical reasoning. By speaking concisely on a subject they have now mastered, the pupils are placed in a more demanding context than that of the small working group.
1 Definition taken from the following article https://www.futura-sciences.com/sciences/definitions/mathematiques-conjecture-373/
As indicated in the previous section, there are two versions for all the conjectures: the blanc version (M1) and the guided version (M2). In the blanc version, students have to navigate through the conjectures without much help. Each problem is posed in the same way in the form of examples – conjecture – proof – theorem, and so the students receive a minimal amount of guidance, but are still left without help when faced with the different sub-sections. In the guided version, there are aids and gap-fill texts to guide the students.
Teachers are free to combine the two versions as they wish:
- blanc version for some students and guided version for others,
- blanc version for the beginning and guided version for the rest,
- blanc version for the first conjectures and guided version for the last conjectures,
- …
-
- Luxembourg context: The University of Luxembourg has a very active mathematics department that is well represented on the international scene. Two of the department’s researchers are featured in the interview in 6 A word from the scientists.
- Differentiation: As described in the previous paragraph, the module contains several levels of differentiation.
- Reference guide for media literacy2
Competences 1: 1.2 Analysing and assessing data, information and digital content.Competences 2: 2.1 Working with others 2.3 Using appropriate forms of expression (netiquette).Competences 3: 3.3 Modelling, structuring and coding. - 4C model: communication, collaboration, creativity, critical thinking: The 4Cs are used in this module. The various questions are solved by group work, which requires communication and collaboration on the part of the students.
- Link with mathematical research: The activities in this module are much closer to mathematical research than the traditional mathematical exercises found in books. This module invites students to “be mathematicians for a day”: to discover mathematical curiosities, formulate them in the form of conjectures and prove them.
2 https://edumedia.lu/wp-content/uploads/2024/12/Medienkompass_EN_web.pdf