Warning: At the end of this module, the usefulness of the weighted sum is demonstrated by stating that it can be used to detect errors in the inversion of two consecutive numbers. The fact that this is only possible when the difference between the two numbers is not equal to 5 is omitted so as not to complicate the reasoning further.
2.5 More on this topic
01
The origins of barcodes
Barcodes were invented in the United States under the name UPC: Universal Product Code. In the beginning of the following video, made by Derek Muller of the Veritasium YouTube channel, the story of barcodes and how the first barcode was scanned on 26 June 1974 is told.
Despite their name, UPC barcodes were by no means universal. They could only be used in the United States. That’s why in Europe, in 1977, a new barcode system was invented called EAN: European Article Number. However, instead of inventing a system to compete with the American system, the EAN extended the American UPC in an ingenious way. The UPC system contains 12 digits, while the EAN system contains 13, but in such a way that an EAN barcode beginning with 0 is equivalent to a UPC barcode without the first 0. In this way, the Americans were able to continue using their system while the rest of the world used EAN barcodes that did not begin with 0. Since 2005, the Americans have also adopted the European version of the barcode, but calling it UPC-13 (Jones, 2009).
02
How barcodes work
In the rest of the text we will restrict ourselves to 13-digit EAN barcodes. This section is mainly based on (Stammbach, 2006).
An EAN number is made up of 4 blocks, the respective meanings of which are detailed below (books and magazines are a special case which will be examined later). The first two digits identify the country of production (Made in…). The next ten digits identify the producing company and the item number within that company.
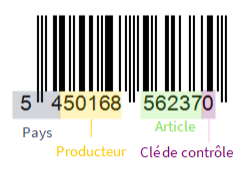
The following table shows the codes for some countries (IREM, 2000).
| États-Unis, Canada | 00-09 |
| France | 30-37 |
| Allemagne | 40-43 |
| Japon | 49 |
| Grande-Bretagne | 50 |
| Belgique | 54 |
| Danemark | 57 |
| Italie | 80-81 |
| Suisse | 76 |
| Autriche | 90-91 |
| Pays-Bas | 87 |
The barcode for LUXLAIT yoghurt, also used in the module, shows that Luxembourg uses the same code as Belgium, probably because of the economic union between the two countries.
As we saw in this module, the 13th digit is a check digit. The algorithm dictates that if \( a_1a_2a_3a_4a_5a_6a_7a_8a_9a_{10}a_{11}a_{12}a_{13} \) is a barcode, then \(a_{13} \) is 10 minus the remainder of the Euclidean division of
\[ a_1+3a_2+a_3+3a_4+a_5+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12} \]
by 10.
In other words
\[ a_1+3a_2+a_3+3a_4+a_5+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12} \]
is a multiple of 10. This can also be expressed in terms of modular calculation:
\[ a_{13} \equiv -(a_1+3a_2+a_3+3a_4+a_5+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12}) \pmod {10} \]This check digit is primarily used to identify reading errors. The reader reads the barcode and uses the algorithm to check that it is the correct barcode. If it is, it beeps and transmits the item and price to the cashier. If the check digit does not obey the algorithm, the reader does not accept the barcode. It has identified the reading error and the item must be re-scanned.
Proposition : Barcodes not only allow the reader to identify a reading error, but also to scan an item even if one of the digits is illegible.
Proof : Let us first assume that one of the odd numbers is unreadable. Without loss of generality, let’s assume that \(a_5\) is unreadable. Let’s go back to the modular equation, and we get:
\[ a_{5} \equiv -(a_1+3a_2+a_3+3a_4+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12}+a_{13}) \pmod {10} \]As \(a_5 \) is a digit (i.e. \( 0 \leq a_5 \leq 9) there is a unique solution to this modular equation.
Now suppose that one of the even numbers is unreadable and, without loss of generality, suppose that \(a_6\) is unreadable. Then we have
\[ 3a_{6} \equiv -(a_1+3a_2+a_3+3a_4+a_5+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12}+a_{13}) \pmod {10} \]Since 3 and 10 are mutually prime, 3 has an inverse modulo 10. n fact, the product of 3 and 7 is 1 modulo 10. By multiplying both sides of the equation by 7, we obtain a value for \(a_6 \) that is unique because \(a_6 \) is a digit.
An attentive reader will note that the previous demonstration remains unchanged without the weighted sum. So what is the point of this weighted sum? It is used to detect a human error that occurs when the cashier has to type in the barcode by hand: the inversion of two consecutive digits.
Proposition : The EAN barcode algorithm detects the inversion of two consecutive digits unless their difference is 5.
Proof : Let \( a_1a_2a_3a_4a_5a_6a_7a_8a_9a_{10}a_{11}a_{12}a_{13} \) be a barcode and invert \(a_i \) et \(a_{i+1} \). If both barcodes are valid barcodes, we have .
\[ \begin{align} a_{13} & \equiv & -(a_1+3a_2+…+a_i+3a_{i+1}+…+3a_{12}) \pmod {10} \\ a_{13} & \equiv & -(a_1+3a_2+…+a_{i+1}+3a_i+…+3a_{12}) \pmod {10} \end{align} \]So we have
\[ a_1+3a_2+ \ldots +a_i+3a_{i+1}+ \ldots +3a_{12}) \equiv a_1+3a_2+ \ldots +a_{i+1}+3a_i+ \ldots +3a_{12} \pmod {10}. \]This equation is equivalent to
\[ 2(a_i -a_{i+1}) \equiv 0 \pmod {10} \]This last equation is true if and only if the difference \(a_i-a_{i+1} \) is a multiple of 5. Since \(a_i\) and \(a_{i+1} \) are digits, the difference is a multiple of 5 if and only if \(a_i = a_{i+1}\) or \( \vert a_i – a_{i+1} \vert = 5\).
Unfortunately, inverting two even-numbered digits or two odd-numbered digits will not be detected by the barcode algorithm.
A safety measure such as the check digit can therefore prevent some errors, but not all. This is always the case. The system is good when it significantly reduces the overall frequency of errors. The more effective it is, the greater the reduction in overall error capacity. To be able to judge this last point, we need to know the prevalence of different types of error. A study based on the English language showed the prevalence of errors when transmitting sequences of numbers (orally or by typing) (Stammbach, 2006):
- Wrong digits accounted for 79.1% of all errors.
- Inverting two consecutive digits accounts for 10.2% of errors.
- All other types of error are less than 1%.
Today, barcodes are not only used to designate products, they are also used – in a modified way – for many other purposes. The reason for this is the wide distribution of the initial system. This meant that the readers could be manufactured in very large numbers and therefore cheaply. So we also find them on all our loyalty cards, library cards and even our CNS card (CNS = Caisse nationale de la santé, in Luxembourg).

03
The ISBN code
When we look at a recent book, we see that it has a barcode, just like supermarket products. By contrast, an older book, published before 2007, has both an EAN barcode and a 10-digit ISBN number.

SBN stands for International Standard Book Number. The ISBN system is based on a principle similar to that of the EAN, but with an extra touch of ingenuity. The 10 elements of the ISBN code take values from 0 to 9 and X represents the number 10 (thanks to the Roman mathematicians). The first nine elements \(a_1 \) to \( a_9 \) uniquely identify the book, and the tenth element
\(a_{10} \) is a check digit obtained as follows
Like the EAN code, the ISBN code detects reading errors and can be used to reconstruct an illegible digit (the evidence is very similar).
However, unlike the EAN code, the ISBN always detects the inversion of any two elements.
Proof : Let’s imagine that the elements \(a_i \) et \(a_k \) have been inverted for \( 1 \leq k \leq 9 \). Then
\[ \begin{align}a_{10} \equiv -(10a_1 + 9a_2 + … +(11-i)a_i + …. + (11-k)a_k + … + 2a_9 ) \pmod {11} \\
a_{10} \equiv -(10a_1 + 9a_2 + … +(11-i)a_k + … + (11-k)a_i + … + 2a_9 ) \pmod {11}
\end{align}
\]
These two equations are equivalent to
\[ (a_i-a_k)(k-i) \equiv 0 \pmod 11. \]Since \( 0 \leq \vert k – i \vert \leq 9 \) and all the numbers between 1 and 9 are prime to 11 (because 11 is a prime number), we have that
\[ a_i-a_k \equiv 0 \pmod 11. \]The elements \(a_i \) and \(a_k \) take values from 0 to 10, which means that \(0 \leq \vert a_i – a_k \vert \leq 10 \). The only solution to the above equation is that \(a_i = a_k \).
Despite the performance of the ISBN code, the ISBN was increased from 10 to 13 digits in 2007 (Stammbach, 2006).
04
IBAN accounts
In Europe, we currently use IBAN (International Bank Account Number) account numbers, an international system for numbering bank accounts. An IBAN consists of up to 34 characters, including :
- The first two characters indicate the country code (for example, LU for Luxembourg, BE for Belgium, DE for Germany, FR for France, etc.),
- The following two characters make up the check digit,
- The last 30 characters or less represent the account number.
The IBAN facilitates transfers and direct debits from one account to another, whether within the same country or between accounts held at banks in different countries.
Unlike the examples seen above, the IBAN has two digits for the check digit. This is not at the end but in the third and fourth positions. The algorithm used to obtain this check digit differs from the previous ones but remains fairly similar (Mathelounge, 2019):
- Consider the IBAN code and remove the two initial letters and the two digits of the check digit.
- Letters are transformed into numbers using the system A=10, B=11, C=12, … (in other words, each letter is replaced by the number that represents it in ASCII minus 55).
- The 4-digit number formed by the two letters is added to the end of the remaining account number.
- The result is an at most 34-digit number.
- The remainder of dividing the number in step 4 by 97 is calculated.
- The two digits of the check digit form the result of 98 minus the remainder obtained in step 5.
In this way, an e-banking system can check whether the account number indicated on a transfer is actually a valid IBAN account number. If it is not, the transfer is refused.
As 97 is a prime number, this system can also be used to find the IBAN number when a digit is illegible.
This reminds me of a story I experienced at the wedding of a mathematician friend of mine. As a present, her friends had put together a sum of money for the couple, but they had planned a series of amusing tests before handing over the precious loot.
Having passed the tests with flying colours, the friends announced with theatrical solemnity that they had deposited the money in a bank account. To access the account, the couple had to use their identity card and the IBAN number of the account. They handed them a sheet of paper with the IBAN number on it… but there was a digit missing!
With a mischievous grin, the friends presented a bowl full of coloured confetti, declaring that the missing number was on one of the confetti. My friend, groaning to the delight of the guests, began searching for the confetti with no chance of success. She and her husband gave up, saying they would look more carefully at home.
Later that evening, she came to me with a knowing smile on her face. I winked at her and told her not to look in that bowl of confetti. She laughed and said she knew, but didn’t want to spoil the surprise for her friends.
So it’s thanks to mathematics that a newly-married couple can earn money without losing their heads in confetti.
05
The QR code
Barcodes are gradually being replaced by their two-dimensional counterparts: QR codes. QR stands for Quick Response. Invented in 1994 by the Japanese company DENSO Corporation to improve the traceability of parts in Toyota factories, QR codes are distinguished by their speed of reading and their resistance to damage, such as oil stains. Today, QR codes are everywhere: from advertisements to web pages and business cards.
However, like other physical means of data storage, QR codes are prone to errors. To ensure that QR code readers can nevertheless process information reliably when errors occur, QR codes do not have one or two check digits, but rely on a more complicated mathematical algorithm known as the Reed-Solomon code. The underlying principle is based on polynomials over finite fields. For more information on QR codes, see the highly instructive article by Down, Sigmon and Klima (2021). Derek Muller of the Veritasium YouTube channel has produced a video explaining QR codes. In it, he builds a QR code from scratch and explains the technology and mathematics behind the invention. At the beginning of the video, he also gives a charming account of the history of barcodes.
References
1. Downs, Adam S., Sigmon, Neil P. and Klima, Richard E. (2021). The Mathematics of QR Codes. Asian Technology Conference in Mathematics https://atcm.mathandtech.org/EP2021/invited/21891.pdf
2. Groupe Lycée, Irem de STRSABOURG. (2000). Clés de contrôle. Repères IREM. 41.
3. Jones, Chris. (2009). How Barcodes Crossed the Atlantic. Mathematics in school 38.5 : 30–31.
4. Mathelounge. (2019). Wissensartikel: Der IBAN-Algorithmus. https://www.mathelounge.de/673376/wissensartikel-der-iban-algorithmus
5. Stammbach, Urs. (2006). EAN, ISBN, CD, DVD: Von Prüfziffern zu fehlerkorrigierenden Codes. Schweizerischer Tag über Mathematik und Unterricht. ETH Zurich.

