Ann Kiefer

To be honest, mathematicians don’t do much. They drink coffee, frown at chalkboards. Drink tea, frown at students’ exams. Drink beer, frown at proofs they wrote last year and can’t for the life of them understand anymore. It’s a life of drinking, frowning, and, most of all, thinking. You see, there are no physical objects in math: no chemicals to titrate, no particles to accelerate, no financial markets to destroy. Rather the verbs of the mathematicians all boil down to actions of thought. […] mathematics is an action of the mind (B. Orlin, 2018). This is the description of mathematicians and/or mathematics given by B. Orlin (2018) in his book Math with Bad Drawings: Illuminating the Ideas That Shape Our Reality.

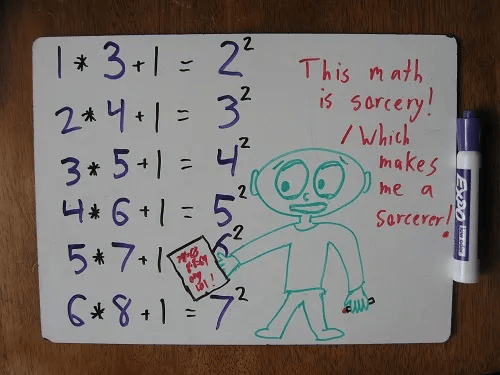
Source: Math with Bad Drawings: https://mathwithbaddrawings.com/2014/01/13/undiscovered-math/

This module gives students the chance to immerse themselves in the role of a mathematician and explore the mindset of mathematical thinking. But what exactly is mathematical thinking?

Music teachers challenge students to listen and participate.
English and History teachers invite students to journey in other worlds.
Art and Drama teachers offer students opportunities to explore.

What are we to offer students if they are to function mathematically? (Gilderdale, 2011)

Unfortunately, many people have a misconception of mathematics, reducing it to simple calculations or multiplication of numbers. In reality, mathematics is a deeply creative discipline that relies more on reflection and written expression than on the complex arithmetic that the general public generally associates with it.

An international research team (Petozc et al. 2007) wanted to find out what first-year university students understood by the term ‘mathematics’. The survey was conducted in Australia, Brunei, Canada, Northern Ireland and South Africa (countries with historical links to the British Empire and education systems derived from the British system). Students from mathematics, engineering and computer science courses were surveyed. The first result: more than half the students defined mathematics primarily as a tool for finding solutions to problems. The authors conclude that there is an urgent need to broaden the scope of mathematics and to give students a broader image of mathematics. The researchers suggest that teachers should not focus solely on techniques in lessons and classrooms, but should show how certain professions use and understand mathematics (math teachers, statisticians, engineers, programmers, etc.). For these professions too, numbers and toolboxes are an integral part of mathematics. But this is just the beginning for them.

We’ve set ourselves the goal of starting this openness to mathematics earlier than university. One of the aims of this module is to show what mathematical thinking, problem solving and proof writing really is, to show how to do these things, and to show how much fun it is. In this module we give (try to give) an answer to this question by breaking with the classic structure of a math lesson, where the teacher explains the theory, does an example on the board in front of the whole class and then the students repeat the same example several times in a ‘drill’ version. Here, the students are given as a starting point a few examples that illustrate a mathematical curiosity. Then it’s up to the students to find more examples themselves and to identify a recurring pattern behind these examples to then formulate a conjecture. Once they have formulated their conjecture, they must try to prove it or find a counterexample. All this work is done in groups, followed by pooling and class discussions. The leitmotif here would be HOTS not MOTS, where HOTS stands for High Order Thinking Skills and MOTS for More Of The Same. This activity will give students the authentic experience of (thinking like) a professional mathematician. Unlike traditional exercises, they will have to explore, analyse and attempt to prove or disprove a theorem based on intriguing observations made previously.

The module “Thinking like a mathematician” should be used in the algebra chapter figuring in the official Luxembourgish school programme for 6e (MENJE, 2023) and aims to model a situation using an algebraic expression. This activity stimulates pupils’ ability to ask themselves the right questions and to “think mathematically”. The concept of mathematical thinking is not new. Pólya was one of the first mathematicians to describe how to solve problems mathematically (Pólya, 1945). Schoenfeld (1985, 1992) then extended these fundamental ideas by identifying several components of mathematical thinking: the knowledge base, problem-solving strategies, metacognition (control and self-regulation) and belief systems. To put it in the words of Stein and Smith (1998):

Tasks that ask students to perform a memorized procedure in a routine manner lead to one type of opportunity for student thinking; tasks that require students to think conceptually and that stimulate students to make connections lead to a different set of opportunities for student thinking.

David Baker, professor of sociology and education at the University of Pennsylvania, agrees:

Overall, there’s a movement towards more complex cognitive mathematics, there’s a movement towards the student being invited to act like a mathematician instead of passively taking in math and science. (Hartnett, 2016).

This is not, of course, an easy exercise, either for the student or for the teacher. The difficulties in understanding, making connections and explaining that students will encounter during this activity are referred to by Schoenfeld (2023) as positive struggle. This is a mechanism for developing a deep and meaningful understanding of mathematical content.

Teachers need to be curious, intrigued and keen to find out more. However they also have to accept messy work, value risk-taking and half-formed ideas, give time to reflect and encourage discussion. (Gilderdale, 2011). The most important thing, however, is that teachers choose the right topics and groups of pupils so that everyone can benefit from the activity and develop their mathematical thinking skills.

The module “Thinking like a mathematician” is also a good example of a TRU activity. TRU stands for Teaching for Robust Understanding and is a framework founded by Alan H. Schoenfeld, a professor at the University of California. It describes the properties of classrooms in which students become powerful and autonomous thinkers in mathematics (Schoenfeld, 2023). The five dimensions of classroom activity are at the heart of TRU. Classrooms that do well in these 5 dimensions produce students who are powerful thinkers:

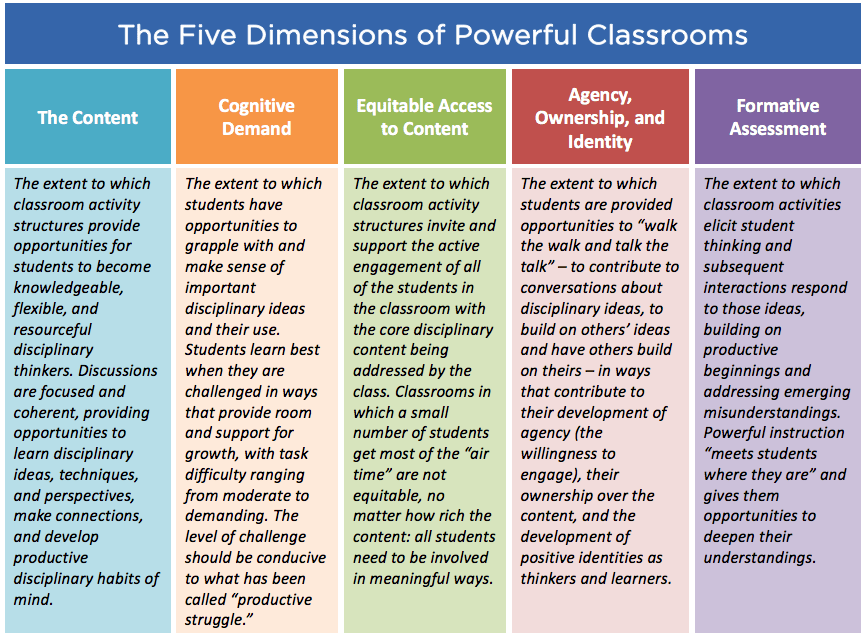
Source: Le cadre de l’TRU en bref, https://truframework.org/

In short, the aim of this module is to show students the abstract, but also the creative and curious, side of mathematics. We hope to change the image of mathematics as boring, pointless and far removed from reality, to a more positive and exciting one.

I don’t expect, and I don’t want, all children to find mathematics an engrossing study, or one that they want to devote themselves to either in school or in their lives. Only a few will find mathematics seductive enough to sustain a long term engagement. But I would hope that all children could experience at a few moments in their careers…the power and excitement of mathematics…so that at the end of their formal education they at least know what it is like and whether it is an activity that has a place in their future. (Wheeler, D. (1975), quoted in Cross, K. (2004)) ³

Some will criticise this module for being too abstract and not showing the applied side of mathematics. To these we reply that other modules in this PITT already do this and, more importantly, we insist that mathematics is not only taught because it is useful. It should be a source of delight and wonder, offering pupils intellectual excitement and an appreciation of its essential creativity (Cross, 2004). ⁴

Références

1. Cross, K. (2004). Engagement and excitement in mathematics. Mathematics Teaching. Vol. 189, pp. 4-7
2. Gilderdale, C. (2011). Generating Curiosity in Mathematics Learning. Nrich. https://nrich.maths.org/5795
3. Hartnett, K. (2016). Meet the New Math, Unlike the Old Math. Quantamagazine. https://www.quantamagazine.org/math-and-science-education-pencils-down-20161005/ 
4. Orlin, B. (2018). Math with Bad Drawings: Illuminating the Ideas That Shape Our Reality. ‎ Black Dog & Leventhal; Illustrated edition.
5. Petocz, P., Reid, A., Wood, L.N., Smith, G.H., Mather, G., Harding, A., Engelbrecht, J., Houston,K., Hillel, J., and Perrett, G. (2007) Undergraduate students’ conceptions of mathematics: an international study. International Journal of Science and Mathematics Education: 5: 439-459
6. Pólya, G. (1945). How to Solve It (2nd edition). Princeton: Princeton University Press.
7. Schoenfeld, A.H. (1985). Mathematical problem solving. Orlando, FL: Academic Press.
8. Schoenfeld, A.H. (1985). Learning ot think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. Grouws (Ed.), Handbook for research on mathematics, teaching and learning, pp. 334-370. New York: MacMillan.
9. Schoenfeld, A.H. (2023). Helping Students Become Powerful Mathematics Thinkers : Case Studies of Teaching for Robust Understanding. New York: Routledge.
10. Stein, M.K. & Smith, M.S. (1998). Mathematical tasks as a framework for reflection. Mathematics Teaching in the Middle School, 3, 268-275.