How do you know whether something is true or not? Surely, you’ve been told that the angles of a triangle add to 180°, for example, but how do you know for sure? What if you met an alien who had never studied basic geometry? How could you convince him/her/it that this fact is true? In a way, this is what mathematics is all about: devising new statements, deciding somehow whether they are true or false, and explaining these findings to other people (or aliens, as the case may be).

[…] As a side note, you might even wonder “What does it mean for something to be true?” A full discussion of this question would delve into philosophy, psychology, and maybe linguistics, and we don’t really want to get into that. The main idea in the context of mathematics, though, is that something is true only if we can show it to be true always. We know 1 + 1 = 2 always and forever. It doesn’t matter if it’s midnight or noon, we can rest assured that equation will hold true. (Have you ever thought about how to show such a fact, though? It’s actually quite difficult! A book called the Principia Mathematica does this from “first principles” and it takes the authors many, many pages to even get to 1 + 1 = 2!) This is quite different from, perhaps, other sciences. If we conduct a physical experiment 10 times and the same result occurs, do we know that this will always happen? What if we do the experiment a million times? A billion? At what point have we actually proven anything? In mathematics, repeated experimentation is not a viable proof! We would need to find an argument that shows why such a phenomenon would always occur. As an example, there is a famous open problem in mathematics called the Goldbach Conjecture. It is unknown, as of now, whether it is true or not, even though it has been verified by computer simulations up until a value of roughly 10¹⁸. That’s a huge number, but it is still not enough to know whether the conjecture is True or False. Do you see the difference? We mathematicians like to prove facts, and checking a bunch of values but not all of them does not constitute a proof.¹

Proof is therefore what makes mathematics different from other subjects and what characterises mathematics. If we were in ancient Greece, the most recent science would tell us that all things are made up of four elements: fire, water, earth and air. It would also tell us that in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides. Today we still believe one of these two facts, but not the other. The difference between the two: the Pythagorean theorem has been proved (Hart, 2024). And a theorem that has been proved once in mathematics, even if its proof is thousands of years old, will remain true forever. This is the great difference between mathematics and the other natural sciences.

Once there is a valid proof of a theorem, that’s enough, in purely mathematical terms. You don’t have to prove it again, and proving it again doesn’t make it ‘truer’. So why do some results have many proofs? The Pythagorean theorem is an example. With hundreds of proofs, it is perhaps the most proven theorem of all time. There are several reasons for this multiplicity of proofs. Firstly, the theorem has been noted in many different cultures. Even ancient Egypt, which probably didn’t know the general result, seems to have known and used the fact that a 3-4-5 triangle has a right angle opposite the longest side. Later, in the Greek, Indian and Chinese traditions, we find different proofs. But even when the proofs of the result were well known, people continued to find new ones. In the case of the Pythagorean theorem, this is something of a mathematical hobby, but sometimes the discovery of another proof of a result can show previously unnoticed connections or potential generalisations. Sometimes, by using a new technique, we realise that it can be applied more widely. Furthermore, it often happens that the first proof of a theorem is not the best – it does the job- but later people find clearer arguments and shorter paths. Over the years, proofs can be refined and simplified so that eventually a beautiful, crystalline kernel remains, where the exquisite genius of the underlying idea is shown to its best effect. (Hart, 2024). Let us consider problem 09 of this module: at first sight it seems that \(n^2+n+41 \) is always prime for any n. In any case, the expression is a prime for n=0,1,2,3,4,5,6,7,8,9,10. So does it always give a prime number? The answer is no (see 1.7 Solutions1.7 Solutions). A first proof of this could be to simply test all the values of n one after the other and realise that at n=40, the expression gives 1681 which is not prime, because 1681 is divisible by 41. A quick way of seeing this divisibility (without using any technological tools) is the following calculation:

This is certainly a completely correct mathematical proof, but it is not very elegant. A more elegant proof is to see that if we take n=41, we obtain a sum of 3 terms each of which is divisible by 41 (the sum being \[ 41^2 + 41 + 41 \]) and so the whole expression is divisible by 41 and therefore does not give a prime number. For more examples of elegant proofs, we recommend that readers watch the lecture A Mathematician’s View of a Proof given by the British mathematician Sara Hart.

1 This text is the beginning of the book Everything You Always Wanted To Know About Mathematics (https://ia600408.us.archive.org/26/items/everything-you-always-wanted-to-know-about-mathematics/bws_book.pdf), which we highly recommend to readers.  

” Mathematics is a vast, ever-growing, ever-changing subject. Among the innumerable questions that mathematicians ask, and mostly answer, some stand out from the rest: prominent peaks that tower over the lovely foothills. These are the really big questions, the difficult and challenging problems, that any mathematician would give his or her right arm to solve. Some remained unanswered for decades, some for centuries, a few for millennia. Some have yet to be conquered.” So begins the book The Great Mathematical Problems written by Ian Stewart (Stewart, 2014).

Fermat’s Last Theorem

One of the best-known problems is Fermat’s Last Theorem. The French mathematician Pierre de Fermat stated this theorem in a marginal note in his copy of Diophantus’ Arithmetica in the 17th century. At one point in this book, the Pythagorean triplets are discussed. In the margin, Fermat writes:

It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.

The modern mathematical statement is as follows:

Fermat’s last theorem. For any integer n>2, there is no non-trivial triple of strictly positive integers \[ (x,y,z) \] such that the following equation is satisfied:

Trivial solutions correspond to cases where one of the terms is zero. For more than three centuries, this theorem remained unproved.

In the Treehouse of Horrors VI episode of The Simpsons, there is a reference to Fermat’s famous theorem.

If the equation behind Homer Simpson were true, a counterexample to Fermat’s Last Theorem would have been found. By calculating, we find that the left-hand side is equal to

2541210258614589…

while the right-hand side is  

Both numbers have 40 digits and the first 9 digits are the same. However, you can see very quickly, without calculation, that this equation cannot be correct because the left-hand side is an odd number while the right-hand side is an even number.

Many mathematicians have tried to prove Fermat’s Last Theorem, but without success. It was not until 1994 that British mathematician Andrew Wiles succeeded in proving the theorem using advanced concepts from number theory and algebraic geometry, in particular elliptic curves and modular forms. The story behind the mathematician Wiles is impressive too. At the age of 10, Andrew Wiles discovered Fermat’s Last Theorem, a centuries-old mathematical puzzle. This encounter marked a turning point in his life, and he vowed to become a mathematician when he grew up and to solve this mystery one day. During his studies in mathematics, Wiles specialised in number theory, a branch that was home to the famous theorem. However, the more he immersed himself in the mysteries of mathematics, the more he perceived the elusive complexity of the problem. The theorem seemed beyond his grasp, and he temporarily abandoned his ambition. But fate sometimes has surprises in store. Other mathematicians made the connection between Fermat’s Last Theorem and elliptic curves and modular forms, subjects in which Wiles had meanwhile become an expert. For seven intense and secret years, Wiles devoted himself wholeheartedly to the proof. In 1994, in a series of lectures, Wiles finally revealed his proof to the world. The announcement caused a sensation, even in the mainstream media – a rare event for a mathematical proof.

Thus, Fermat’s Last Theorem, which had haunted minds for centuries, was finally answered thanks to the tenacity and ingenuity of Andrew Wiles. Wiles’ proof has had a profound impact on mathematics. It opened up new perspectives in number theory and strengthened our understanding of elliptic curves and modular forms. Fermat’s Last Theorem is now an emblematic example of the power of mathematics and the perseverance of researchers (Stewart, 2014). For a more extensive history of Fermat’s Last Theorem, we recommend Simon Singh’s incredible book Fermat’s Last Theorem (Singh, 2002). A nice summary of the history of Fermat’s Last Theorem is also given in the first 30 minutes of the podcast Dernier Théorème de Fermat : à l’épreuve de l’informatique from France Culture’s series La Science, CQFD, mentioned at the end of section 03 And what about artificial intelligence?

Kepler’s conjecture

Another well-known conjecture that took several hundred years to solve is the Kepler conjecture. In 1611, the astronomer Johannes Kepler, who had begun studying arrangements of spheres, stated his conjecture:

Kepler’s conjecture. The close packing is the densest possible sphere packing.

To explain this in a simpler way, let’s consider a large empty space, such as an aircraft hangar, and ask ourselves what is the greatest number of balls that can be placed in it. If, instead of balls, we try stacking identical wooden blocks, like children’s building blocks, the answer becomes easy. The cubes fit together with no wasted space and we can fill almost one hundred per cent of the space (ignoring the small amount of space that may be left around the walls and ceiling). Hence the number of cubes we can stack is almost equal to the volume of the shed divided by the volume of one of the cubes.

But spheres don’t fit together as well as cubes, and there is always wasted space in between. No matter how ingeniously the balls are arranged, about a quarter of the space will go unused. A familiar arrangement is as follows:

Source: Source : Empilement compact de plans compact (Conway & Sloane, 1999)

In 1611, Kepler claimed that this arrangement was in fact the most optimal stack in existence. He was convinced of this but was unable to prove it. It was only in 1998 that Thomas Hales announced that he had proved the conjecture. His proof was very long and computer-assisted. It was extraordinarily difficult to verify but is now fully verified and accepted by the mathematical community. The story didn’t end there, because the question of an optimal stacking of spheres can arise in any dimension (and not just dimension 3). This more general problem is known as the Sphere Packing Problem. The optimal solution in dimension 2 is as follows:

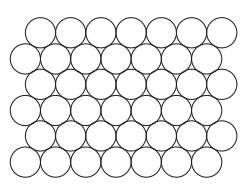
Optimal stacking in dimension 2 was only proved in 1940. For higher dimensions, the problem was recently solved for dimensions 8 and 24 by the Ukrainian mathematician Maryna Viazovska (Klarreich, 2016).

Source: : https://www.faz.net/aktuell/wissen/falling-walls/die-mathematikerin-maryna-viazovska-gewinnerin-der-fields-medaille-im-gespraech-18452365.html/

For all other dimensions (dimensions strictly greater than 3 and different from 8 and 24), the optimal stacking is not yet known.

The twin primes conjecture

A third conjecture we wanted to talk about is the twin primes conjecture.

Definition. Let \(p_1\) and \(p_2\) be two prime numbers. We say that \(p_1,p_2\) form u pair of twin primes if 

\[ p_2-p_1=2. \]

The first pairs of twin primes are

(3,5),(5,7),(11,13),(17,19),…

We have known since Euclid (300 BC) that there are an infinite number of prime numbers. The question that then arises, and that mathematicians have been asking since the 19th century, is whether there is also an infinite number of twin primes. As the proof of the infinity of primes is relatively simple, mathematicians initially thought that the proof of the infinitude of twin primes could not be very complicated either. But no one could find a proof. Of course, computers were finding bigger and bigger twin primes. The largest known to date are

This pair was discovered in 2016. We also know that there are 808,675,888,577,436 twin primes with less than 18 digits. All these facts mean that mathematicians are convinced that there is indeed an infinite number of twin primes. However, as we saw in the previous paragraph, being convinced or finding a large number of examples that work does not constitute proof in mathematics. In May 2013, everything changed with the publication of an article by mathematician Yitang Zhang. In the article he proved the following theorem.

Theorem (Zhang, 2013). here are infinitely many primes \(p_1,p_2\) such that
\[ p_2-p_1 \leq 70.000.000. \]

This theorem caused a sensation in the mathematical world. Why did it cause such a stir? Until 2013, nothing was known about twin primes. Mathematicians were convinced that there were infinitely many, but they had no proof. So it could be that the prime numbers were getting further and further apart: that after a certain huge number, we would no longer find twin primes, and then after an even bigger number, we would no longer find primes with a distance of 4, and then 6, and so on. This was a real possibility. In 2013, Zhang demonstrated that if we give ourselves the number 70,000,000 as an upper limit, then we will always find primes that are at most 70,000,000 apart as far down the number line as we go. Let’s face it, 70,000,000 is not at all equal to 2, but the two numbers aren’t that different either, in the sense that Zhang’s theorem was a first step in the right direction. In the year that followed, several other mathematicians, including Terence Tao (see next section), succeeded in reducing the number from 70,000,000 to 246, which gives the current theorem :

Theorem (Maynard, Polymath, Tao, 2014). There are infinitely many primes \(p_1,p_2\) such that
\[ p_2-p_1 \leq 246. \]

The limit 246 is already closer to 2 than the previous limit, but unfortunately Tao and Maynard have also shown that with the methods applied so far, it will be impossible to reduce this limit any further. So a new idea or new methods will have to be found mathematically, which means that although there has been a breakthrough in the twin primes conjecture, the conjecture remains open.

Other well-known open conjectures are those illustrated in problems 13 and 14 of this module.

The Goldbach conjecture

Problem 13 is known as the Goldbach conjecture, formulated in 1742 by Christian Goldbach.

Goldbach conjecture . Any even integer greater than 3 can be written as a sum of two primes.

This is one of the oldest open conjectures in mathematics. It is verified for any even number less than
\(4 \cdot 10^{18} \), but remains open in general. There is a weak version of Goldbach’s conjecture, which states that any odd number greater than 9 can be written as the sum of three primes. This version is called the weak version, because if Goldbach’s conjecture is proved one day, the weak version follows straight away: every odd number a greater than 9 is written as the sum of an even number b and 3. So if b is written as the sum of two primes (by Goldbach’s conjecture), a is written as the sum of these two primes and 3, so 3 primes.
In 2013, the Peruvian mathematician Harald Helfgott published a proof of the weak version. This proof has still not been verified.

Source: xkcd https://xkcd.com/1310//

Terence Tao, whom we have already met several times, has proved the following theorem.

Theorem (Tao, 2012). Any odd integer greater than 1 can be written as a sum of at most five primes.

Goldbach’s conjecture is part of problem 8 of Hilbert’s problems, together with the twin primes conjecture and the Riemann hypothesis. The Riemann hypothesis is probably the best-known conjecture in mathematics. This seemingly anecdotal hypothesis put forward by Bernhard Riemann one hundred and fifty years ago concerns the distribution of prime numbers. A fascinating and understandable summary is given in the book The Music of the Primes by mathematician Marcus du Sautoy (du Sautoy, 2003). The following video provides a very brief summary.

At the Second International Congress of Mathematicians, held in Paris in August 1900, David Hilbert presented a list of problems that had hitherto challenged mathematicians. According to Hilbert, these problems were to mark the development of mathematics in the 20th century, and it is undeniable that they had a considerable impact. After the congress, the final list included 23 problems, known today as Hilbert’s problems. Today, 8 of these problems are completely solved, 10 have partial solutions and 5 are still unsolved. A funny anecdote is that Hilbert expressed somewhat contradictory opinions about the difficulty of the Riemann hypothesis. At one point he compared three unsolved problems: the transcendence of \(2^{\sqrt{2}}\), Fermat’s Last Theorem and the Riemann Hypothesis. According to him, the Riemann Hypothesis would probably be solved in a few years, Fermat’s Last Theorem perhaps in his lifetime, and the transcendence question perhaps never. Surprisingly, the question of transcendence was resolved a few years later. As seen before, Andrew Wiles recently proved Fermat’s Last Theorem and Riemann’s hypothesis remains open. On another occasion, Hilbert remarked that if he woke up after a sleep of five hundred years, his first question would be whether the Riemann hypothesis had been solved (Conray, 2003).

The 21st century equivalent of Hilbert’s problems is the list of seven Millennium Prize problems selected in 2000 by the Clay Institute of Mathematics. Unlike the Hilbert problems, for which the main reward was the admiration of David Hilbert himself and mathematicians in general, each of the prize problems comes with a $1 million prize. To date, only one of the seven problems has been solved. It is the Poincaré conjecture, which has been solved by the eccentric Russian mathematician Grigori Perelman.

The Collatz conjecture

Problem 14 in this module is known in the mathematical world as the Collatz or Syracuse conjecture. This conjecture is not one of the great mathematical problems, but it has become part of mathematical folklore because, despite the simplicity of its statement (it can be explained to a primary school child), this conjecture has been challenging mathematicians for many years.

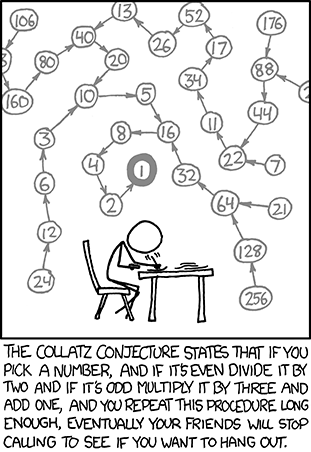
The following video by Derek Muller of the Veritasium YouTube channel provides more information.

The Euler conjecture

Just as in this module, there have also been conjectures in the history of mathematics that mathematicians were convinced were true, but which turned out to be false in the end. A well-known example of this is the Euler conjecture, which was originally proposed by the Swiss mathematician Leonhard Euler in 1772 and which reads as follows:

Euler’s conjecture. For any integer n strictly greater than 2, the sum of n-1 nth powers is not an nth power.

Note that the case n=3 corresponds to Fermat’s Last Theorem with exponent 3. It was only in 1966 that two mathematicians found a counterexample and wrote one of the shortest articles ever published in mathematics:

Source:https://www.ams.org/journals/bull/1966-72-06/S0002-9904-1966-11654-3/S0002-9904-1966-11654-3.pdf/

The Pólya conjecture

A final example of a refuted conjecture is Polya’s conjecture. We’ll start with a definition.

Définition. A positive integer is called of even type if its prime factorisation contains an even number of prime factors. Otherwise it is called of odd type.

Let’s do an example. Take \(15=3 \cdot 5\). The number 15 has 2 prime factors and is therefore of even type. On the other hand \(12=2\cdot 2 \cdot 3 \)and therefore 12 is of odd type.

By definition, 1 is of even type and all primes are of odd type.

Definition. E(n) denotes the number of positive integers less than or equal to n which are of even type and O(n) the number of positive integers less than or equal to n which are of odd type.

Let’s try to determine E(9) and O(9).Take all the positive integers from 1 to 9 inclusive and decide whether they are of even or odd type.

• The numbers 1, 4, 6 and 9 are of even type. There are 4 in all. So E(9)=4.
• The numbers 2, 3, 5, 7 and 8 are of odd type. There are 5 in all. So O(9)=5.

Polya conjecture. For any integer \(n \geq 2 \), E(n) is less than or equal to O(n).

Is there a proof for Polya’s conjecture?

The answer is … no!

In 1962, Sherman Lehman found that this conjecture fails for n=906 180 359. The smallest counterexample is n=906 150 257 and was discovered by Minoru Tanaka in 1980.

Polya’s conjecture is therefore false.

And finally, a quote from Polya about teaching mathematics:
A teacher of mathematics has a great opportunity. If he fills his allotted time with drilling his students in routine operations he kills their interest, hampers their intellectual development, and misuses his opportunity. But if he challenges the curiosity of his students by setting them problems proportionate to their knowledge, and helps them to solve their problems with stimulating questions, he may give them a taste for, and some means of, independent thinking.

Proofs involving computer calculations have been around for some time. The most famous is the proof of the four-colour theorem. The four-colour theorem states that it is possible, using only four different colours, to colour any map divided into regions, so that two adjacent regions, i.e. those that have an entire border (and not just a point) in common, always receive two distinct colours.

The result was conjectured in 1852 by Francis Guthrie, who was interested in colouring the map of the regions of England. Two early claimed proofs were published, by Alfred Kempe in 1879 and Peter Guthrie Tait in 1880. But they proved to be wrong; the errors were only identified in 1890.

Although Kempe’s proof turned out to be false, it does provide a proof of a similar problem, with five colours instead of four, known today as the five-colour theorem.

In 1976, two Americans, Kenneth Appel and Wolfgang Haken, claimed to have demonstrated the four-colour theorem. Their proof shocked the scientific community: for the first time, a proof required the use of a computer. The two mathematicians had succeeded in reducing the infinite number of possible maps to exactly 1,482. To check that these 1,482 cases could all be coloured with just 4 colours, they wrote a computer program that tested the 1,482 cases one by one (over 1,200 hours of calculation). Since 1976, other computer programs, written independently of the first, have produced the same result.

To this day, no proof has been discovered that can do without a computer; however, many enthusiasts continue to be convinced that they have proved the Four Colour Theorem without a computer. In the book Mathematical Cranks (Underwood, 1992), a whole chapter is devoted to these sometimes very funny attempts.

So how do we know that the proof of the Four Colour Theorem is correct? Are these computer proofs valid? For most mathematicians, yes. The reason is that, as long as we check the program, the risk of a stray neutrino turning a 0 into a 1 and producing an erroneous result seems smaller than the risk of there being an error in one of the hundreds of pages of hand-written proofs (such as Fermat’s theorem). Human beings are considerably more fallible than machines, if we correctly asked the machine to do what we wanted it to do. Proofs done by hand, where anyone (with sufficient mathematical knowledge) can check the proof line by line, are of course still preferable, but such proofs are sometimes hard to find. In this case a computer proof is better than no proof (Hart, 2024).

Now, with recent advances in artificial intelligence, the question arises as to whether computers will soon be able to prove theorems on their own, without the help of a human being. According to Fields Medal winner Terence Tao, we’re not there yet. In an interview with Quanta Magazine, he states that artificial intelligence tools are not yet capable of doing the high-level mathematics of current research. However, he is convinced that it will come (Strogatz, 2024).

I think, the next cultural shift will be whether AI-generated proofs will be accepted. Right now, AI tools are not at the level where they can generate proofs to really advance mathematical problems. Maybe undergraduate-level homework assignments, they can kind of manage, but research mathematics, they’re not at that level yet. But at some point, we’re going to start seeing AI-assisted papers come out and there will be a debate. – Terence Tao, 2024. 

There are currently projects aimed at formalising the proofs of major theorems in what are known as formal proof assistants. These are computer languages capable of checking whether a proof is true or not, and therefore whether the theorem has been proved or not (Strogatz, 2024). These assistants will enable many more mathematicians to work together. For the moment, a collaboration on a project never contains more than 5 mathematicians. In a collaboration, you either have to trust the other mathematicians completely, or check all their calculations and proofs line by line. With more than 5 people, this becomes too chaotic. But once these formal proof assistants are in place, much larger collaborations are entirely possible, because these tools will check the different steps (Drösser, 2024).

An example of such an assistant is given in the podcast  Dernier Théorème de Fermat : à l’épreuve de l’informatique from France Culture‘s series La Science, CQFD. The podcast talks about a proof assistant that is verifying the proof of Fermat’s Last Theorem mentioned earlier. The first 30 minutes of the podcast provide a nice summary of the history of Fermat’s Last Theorem.

References

1. Conrey, J.B. (2003). The Riemann Hypothesis. Notices of the American Mathematical Society. Volume 50. Number 3. https://www.ams.org/notices/200303/fea-conrey-web.pdf
2. Conway, J. H. and Sloane N. J. A. (1999) Sphere Packings, Lattices and Groups. Third edition. New York: Springer.
3. Drösser, C. (2024). AI Will Become Mathematicians’ ‘Co-Pilot’. Scientific American. June 2024. https://www.scientificamerican.com/article/ai-will-become-mathematicians-co-pilot/
4. Hart, S. (2024). A Mathematician’s View of Proof. Gresham College Lecture Series. https://www.gresham.ac.uk/watch-now/mathematician-proof
5. Klarreich, E. (2016). Sphere Packing Solved in Higher Dimensions. Quanta Magazine. https://www.quantamagazine.org/sphere-packing-solved-in-higher-dimensions-20160330/
6. Du Sautoy, M. (2003). The Music of the Primes. Harper.
7. Singh, S. (2002). Fermat’s Last Theorem. London: Fourth Estate.
8. Stewart, Ian. (2014). The Great Mathematical Problems : Marvels and Mysteries of Mathematics. London: Profile Books.
9. Strogatz, S. (2024). What makes for Good Mathematics? The Joy of Why. Quanta Magazine. https://www.quantamagazine.org/what-makes-for-good-mathematics-20240201/
10. Sullivan, B.W. (2013). Everything You Always Wanted To Know About Mathematics (But didn’t even know to ask). A Guided Journey Into the World of Abstract Mathematics and the Writing of Proofs. https://ia600408.us.archive.org/26/items/everything-you-always-wanted-to-know-about-mathematics/bws_book.pdf
11. Underwood, D. (1992). Mathematical Cranks. The Mathematical Association of America, Washington, 1992, v + 372.
12. Whitehead, A. N., and Russell, B. (1997). Principia Mathematica. Second edition. Cambridge: Cambridge University Press.