Public visé : 6^e C et G
Local : une salle de classe usuelle
Matériel nécessaire : au moins un ordinateur ou tablette avec accès à l’internet par groupe de 2 élèves.
Durée : 3-4 fois 45 minutes

Compétences visées par le cours de mathématiques

Contenus

• Choisir un type de graphique
• Interprétation graphique
• Créer un sondage
• Interpréter les résultats d’un sondage

L’élève est capable de/d’

• construire un tableau de valeurs, un graphique/diagramme évolutif, un graphique/diagramme en bâtonnets, un graphique/diagramme circulaire
• choisir le graphique/diagramme adéquat pour représenter des données
• réaliser une enquête en utilisant des outils digitaux
• utiliser un tableur pour analyser des données et pour les visualiser à l’aide d’un graphique

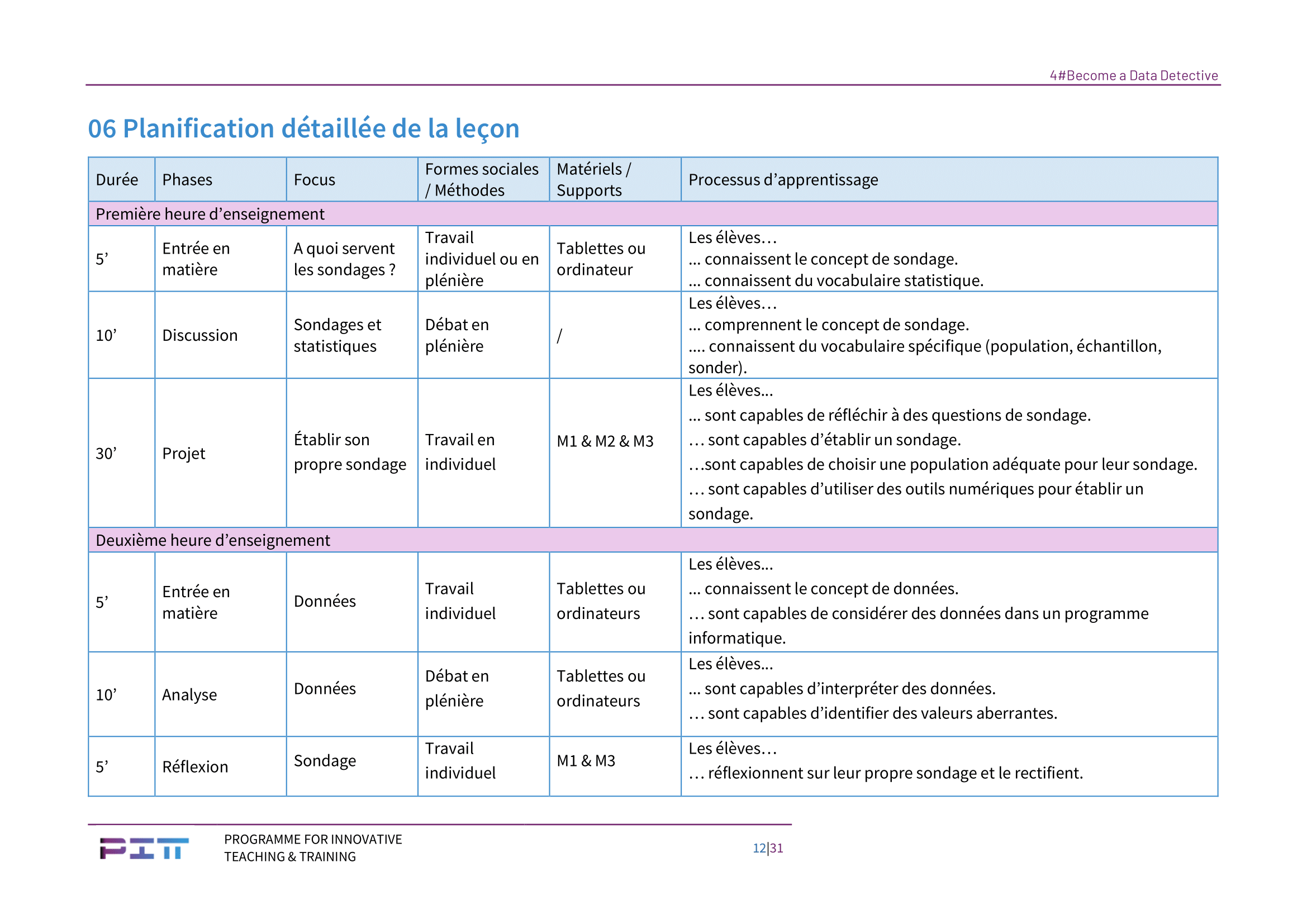
Première Leçon

Entrée en matière (5 min). Les élèves regardent la vidéo Youtube courte, intéressante et adaptée à leur niveau :

Discussion (10 minutes). Les éléments clés de la vidéo (poser des questions, sélectionner des gens qui représentent la population, échantillon, observer l’opinion publique etc.) sont discutés en plénière.

Établir son propre sondage (30 min). Les élèves établissent leur propre sondage. Ils choisissent une population cible (les élèves de la classe, de l’école, les amis, toute la population de leur village, leur pays etc.). Puis ils formulent (au moins) 6 questions visant à découvrir l’opinion de leur population cible sur un thème quelconque. Pour chaque question, ils doivent réfléchir si c’est une question

• à choix multiple,
• à réponse ouverte,
• à opinion
• …

et aux différentes réponses possibles, le cas échéant (M1). Puis les élèves créent un sondage dans Microsoft Forms. Tout autre logiciel est permis aussi. Nous avons opté pour Microsoft Forms car les élèves et enseignants y ont accès via Microsoft 365 Copilot (anciennement Office 365). Il y a trois options :

1. Les élèves peuvent faire leur propre sondage.
2. Ils peuvent utiliser un sondage fait par nous.
3. Ils peuvent adapter le sondage fait par nous.

Les explications techniques relatives au sondage sont en M2.

Devoir à domicile. Finir la création du sondage et faire remplir le sondage par des amis, des camarades d’écoles, la famille etc.

Deuxième leçon

Entrée en matière (5 min). On laisse 5 minutes aux élèves pour contempler leurs données récoltées.

Analyse des données (10 min). Discuter en plénière des données récoltées par les élèves : est-ce que toutes les données correspondent à l’attente de la question ? Est-ce que les questions auraient pu ou dû être posées différemment. Est-ce que les réponses possibles auraient dû être formulées différemment ?

Différenciation : pour les élèves avancés, une discussion sur des possibles outliers (ou valeur aberrante en français ; valeur ou une observation qui est « distante » des autres observations effectuées sur le même phénomène) peut avoir lieu ainsi qu’une réflexion sur quoi faire avec ces données.

Rectification du sondage (5 min). Les élèves reprennent le tableau M1 (M3) et reformulent les questions de leur sondage.

Question de recherche (15min). Répartir la classe en équipes de 3 à 4 élèves. Nous conseillons de favoriser des équipes qui travaillent bien ensemble et pas multi-niveau : faibles ensemble et forts ensemble¹. De cette manière les échanges sont favorisés. Chaque équipe réfléchit à une question de recherche statistique intéressante qui remplit les conditions suivantes :

1. impossible de répondre à la question par oui/non,
2. obligation de combiner deux questions du sondage,
3. question intéressante pour les élèves.

Voilà quelques exemples basés sur notre sondage :

• Qui passe plus de temps devant un écran, les filles ou les garçons ?
• Est-ce que ceux qui possèdent un IOS passent plus de temps devant l’écran ou est-ce que les autres passent plus de temps devant l’écran ?
• Quel est le lien entre l’âge de la personne et l’activité principale sur son smartphone ?
• Est-ce que les gens possédant un IOS, un Android ou un Windows smartphone possèdent plus de télés à la maison ?

Question de recherche 2 (10 min). Mise en commun (dans un google doc) de toutes les questions de recherche statistique possibles et retenue d’une des questions (discussion + vote). La discussion peut porter (entre autres) sur

• intérêt,
• pertinence,
• formulation (clarté).

Le vote peut avoir lieu en anonyme ou par lever de main.

Troisième leçon

Entrée en matière (5 min). Répétition de la question de recherche choisie par vote à la leçon précédente.

Résultat (15 min). Résolution de la question au sein de l’équipe.

Instructions pour les élèves :

1. Attention aux outliers (voir plus haut).
2. Trouver une réponse à la question en utilisant les données.
3. Faire un graphique.

Instructions pour l’enseignant :

1. circuler et voir ce que les élèves font
2. faire signe à une équipe s’ils ne considèrent pas les outliers, travaillent avec des données non adéquates etc.

Formulation du résultat (15 min). Les élèves formulent une réponse à leur question de recherche en faisant un graphe et en écrivant un texte court. Les élèves peuvent utiliser le graphe fait automatiquement par Microsoft Forms. Ils peuvent également exporter les réponses dans Excel (voir M3) pour ensuite faire un graphe personnalisé. N’importe quel autre programme ou tableur est possible aussi.

Présentations I (10 min). Chaque équipe présente ses résultats au tableau (choix : porte-parole ou tous ensemble), leur graphique à l’appui. Ils sont demandé également de présenter leur méthode d’analyse.

Les autres élèves peuvent réagir aux résultats des autres équipes et poser des questions. L’enseignante fait des commentaires sur le graphique (couleurs utilisés ? Label des axes ? Titres ? Claire ?).

Quatrième leçon

Présentation II (10 min). Finir les présentations commencées dans la troisième leçon.

Wrap up (15 min). Lors de la plénière, l’enseignant guide les élèves dans une analyse comparative des différentes stratégies employées par chaque groupe. Il insiste explicitement sur le fait que des réponses divergentes peuvent toutes être valables dans ce contexte. L’enseignant met en évidence que chaque méthode présente ses propres forces et faiblesses. Il rappelle que ce module se distingue par l’absence d’une solution unique et définitive.

Si le temps le permet, l’enseignant orchestre une discussion métacognitive amenant les élèves à réfléchir à cette particularité de la statistique : pourquoi accepte-t-elle plusieurs réponses correctes, contrairement aux mathématiques qu’ils pratiquent habituellement à l’école ? Cette réflexion leur permettra d’approfondir leur compréhension épistémologique des disciplines et de développer leur pensée critique face aux différentes formes de raisonnement scientifique.

1 Certaines recherches récentes en didactique des mathématiques ont montré que dans les groupes mixtes ou multi-niveaux, les élèves forts ont tendance à dominer les discussions en équipe et à prendre des décisions importantes concernant les mathématiques à travailler, alors que les élèves plus faibles se chargent davantage des tâches davantage procédurales (prendre des notes, etc.).

L’enseignant notera que cette unité permet une différenciation naturelle adaptée aux différents niveaux des élèves. Pour les apprenants les plus avancés, il est recommandé de les encourager à approfondir leur réflexion statistique en explorant les concepts plus complexes comme l’identification et le traitement des valeurs aberrantes (outliers).

L’enseignant peut les guider à se questionner sur l’impact de ces valeurs sur leurs résultats, les méthodes appropriées pour les détecter et les différentes stratégies pour les traiter (inclusion, exclusion, transformation des données).

La flexibilité intrinsèque de ce module constitue l’un de ses principaux atouts pédagogiques. En permettant aux élèves de concevoir leur propre sondage et de formuler leurs questions de recherche selon leurs capacités et leurs intérêts, le module s’adapte naturellement aux différents niveaux de compétence présents dans la classe.

Cette structure ouverte offre plusieurs avantages :

• Les élèves ayant besoin de plus de soutien peuvent travailler sur des problématiques plus accessibles.
• Les élèves plus avancés peuvent s’engager dans des analyses statistiques plus sophistiquées.
• Chaque groupe peut progresser à son rythme tout en participant au même projet global.
• L’enseignant peut différencier son accompagnement selon les besoins spécifiques identifiés.

Cette différenciation automatique intégrée au design même de l’activité permet à l’enseignant de créer un environnement d’apprentissage inclusif où chaque élève est stimulé à son niveau optimal de développement.

1. Contexte luxembourgeois : L’équipe MIDAS de l’Université du Luxembourg, mené par Prof. Christophe Ley, fait des recherches sur la modélisation, la science des données, les mathématiques appliquées et les statistiques. Entre autres, ils font des projets interdisciplinaires autour de statistiques et sport.
2. Différenciation : Comme décrit dans le paragraphe précédent, le module contient plusieurs niveaux de différenciation dans le choix même de la version de l’histoire mais aussi dans les exercices proposés.
3. Guide de référence pour l’éducation aux et par les médias¹ :
   Compétences 1 : 1.1 Filtrer et rechercher des données, des informations et des contenus numériques, 1.2 Analyser et évaluer des données, des informations et des contenus numériques, 1.4 Traiter des données, des informations et des contenus numériques
   Compétences 2 : 2.1 Interagir avec autrui, 2.2 Partager et publier des données, des informations et des contenus numériques
   Compétences 3 : 3.3 Modéliser, structurer et coder
4. Modèle des 4C : communication, collaboration, créativité, pensée critique : Les 4C interviennent dans ce module. Les différentes questions se résolvent en travail de groupe, ce qui demande de la communication et collaboration de la part des élèves. L’idée principale de ce module autour des données et des statistiques est le développement de la pensée critique.
5. Lien avec la recherche en mathématiques : Les données sur le foot utilisées dans ce module sont les mêmes données que celles que Prof. Christophe Ley utilise avec son équipe pour établir les modèles d’intelligence artificielle qui prédisent les résultats des coupes du monde (voir 4.5 Pour aller plus loin et 4.6 La Parole aux scientifiques pour plus de détails).

1 https://edumedia.lu/wp-content/uploads/2024/12/Medienkompass_FR_web.pdf 

Télécharger le PDF