Le jeu peut être emprunté au Centre de documentation pédagogique de l'IFEN ou au F.use (Future Space for Education) au Campus Belval.
1.2 Planification de l’unité
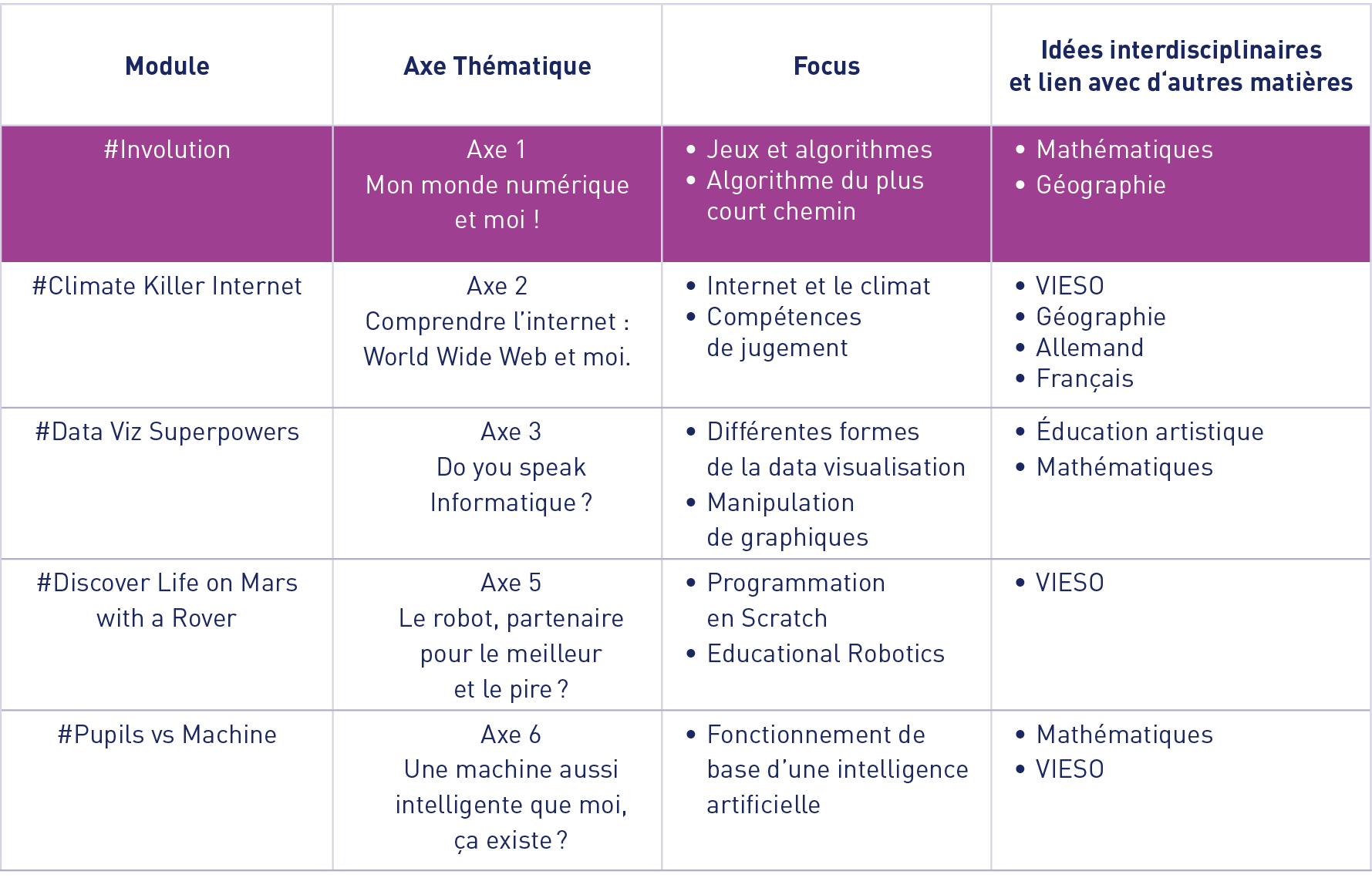
01
Sujet de l’unité dans la structure globale des axes
Comme les modules sont indépendants les uns des autres, il n’est pas nécessaire d’avoir pris connaissance des autres modules pour traiter celui-ci.
Ce module a été conçu en collaboration avec Hugo Parlier et Bruno Teheux du département de mathématiques de l’Université du Luxembourg.
02
Modalités de l’unité
- Public visé : 7e-5e classique et générale
- Local : pas de local spécial à prévoir
- Matériel nécessaire :
- Le jeu Involution© : le jeu peut être emprunté au Centre de documentation pédagogique de l’IFEN ou au F.use (Future Space for Education) au Campus Belval.
- Des ordinateurs ou tablettes peuvent être utilisés pour lire les instructions, Ces dernières peuvent aussi être tout simplement imprimées.
- Durée : 2 heures d’enseignement
03
Contextualisation des Savoirs
L’objectif principal de la leçon est de donner corps aux notions d’algorithme vues en cours via Involution© : un jeu ou casse-tête développé par Hugo Parlier et Bruno Teheux, deux chercheurs en mathématiques de l’Université du Luxembourg. Par le biais de ce jeu, les élèves se familiarisent avec des concepts mathématiques et algorithmiques comme l’algorithme du plus court chemin, les stratégies optimales et non optimales, le tout de manière ludique. Le jeu consiste en une rangée de 10 anneaux noirs et blancs. Une manivelle en forme de cercle est placée sur le jeu et par un mouvement de rotation, les anneaux changent de position. Le but du jeu est de changer la position des anneaux afin d’obtenir une configuration donnée à partir d’une configuration de départ.
04
Transposition didactique
a. Objectifs d’apprentissage et compétences visées
b. Justification didactique
c. Réduction didactique
Compétences visées de l’Axe 1 : Mon Monde Numérique et Moi !
- SAVOIRS : connaissances de base du vocabulaire numérique et informatique général, de la communication entre humain et outil informatique (notion d’algorithme) et du principe d’abstraction en matière de résolution de problèmes.
- SAVOIR-FAIRE : décomposition d’un problème à des fins de résolution, conception et représentation d’un algorithme, élaboration et application d’un algorithme simple avec des cartes et d’un déroulement de programme.
- SAVOIR-ÊTRE : prise de conscience de l’implication de l’informatique dans les tâches quotidiennes en fonction des choix en matière d’outils, d’informations fournies et des résultats obtenus.
Compétences visées du Guide de référence pour l’éducation aux et par les médias1
- Compétences 2 – Communication et collaboration : 2.1 Interagir avec autrui
- Compétences 3 – Créer des contenus : 3.3 Modéliser, structurer et coder
L’objectif de ce module est que les élèves comprennent la notion et le fonctionnement des algorithmes à travers un jeu. Une des particularités du module est de n’utiliser ni technologie électronique, ni ordinateur, ni tablettes. Ces activités, dites « débranchées », servent souvent à initier à la pensée informatique pour « se libérer de la complexité technologique lors de l’apprentissage et découvrir les notions fondamentales en informatique » (INRIA, 2020). L’accès est donc aisé et permet de comprendre un aspect essentiel du numérique : les cultures numériques n’ont en premier lieu rien à voir avec les ordinateurs au sens de machines électriques – la caractéristique de l’algorithmicité, par exemple, qui est au cœur de ce module, peut être décrite par la formation de modèles mathématiques et logiques formels, qui peuvent également être représentés de manière mécanique. Pour citer l’informaticien Leslie Lamport : « L’importance de réfléchir et d’écrire avant de coder doit être enseignée dans les cours d’informatique de premier cycle et elle ne l’est pas » (Han, 2022).
Ainsi, le module #Involution s’appuie sur les bases du codage enseignées dans le Fondamental et les développe, à la croisée des mathématiques et de l’informatique.
Involution© propose plusieurs défis de type « shortest path » de différents niveaux et les situe dans le cadre de l’apprentissage coopératif et de la résolution de problèmes. Le jeu stimule un processus cognitif ciblé qui peut être développé activement à partir du matériel pédagogique distribué. La planification et la mise en œuvre de l’unité d’enseignement peuvent faire totalement abstraction d’une répartition stricte du temps au profit d’une expérimentation libre avec Involution© et les instructions mises à disposition. La consolidation des connaissances et des compétences se fait par le biais de l’apprentissage par l’enseignement, les élèves présentant à la classe leurs solutions ainsi que les raisons de leur choix.
05
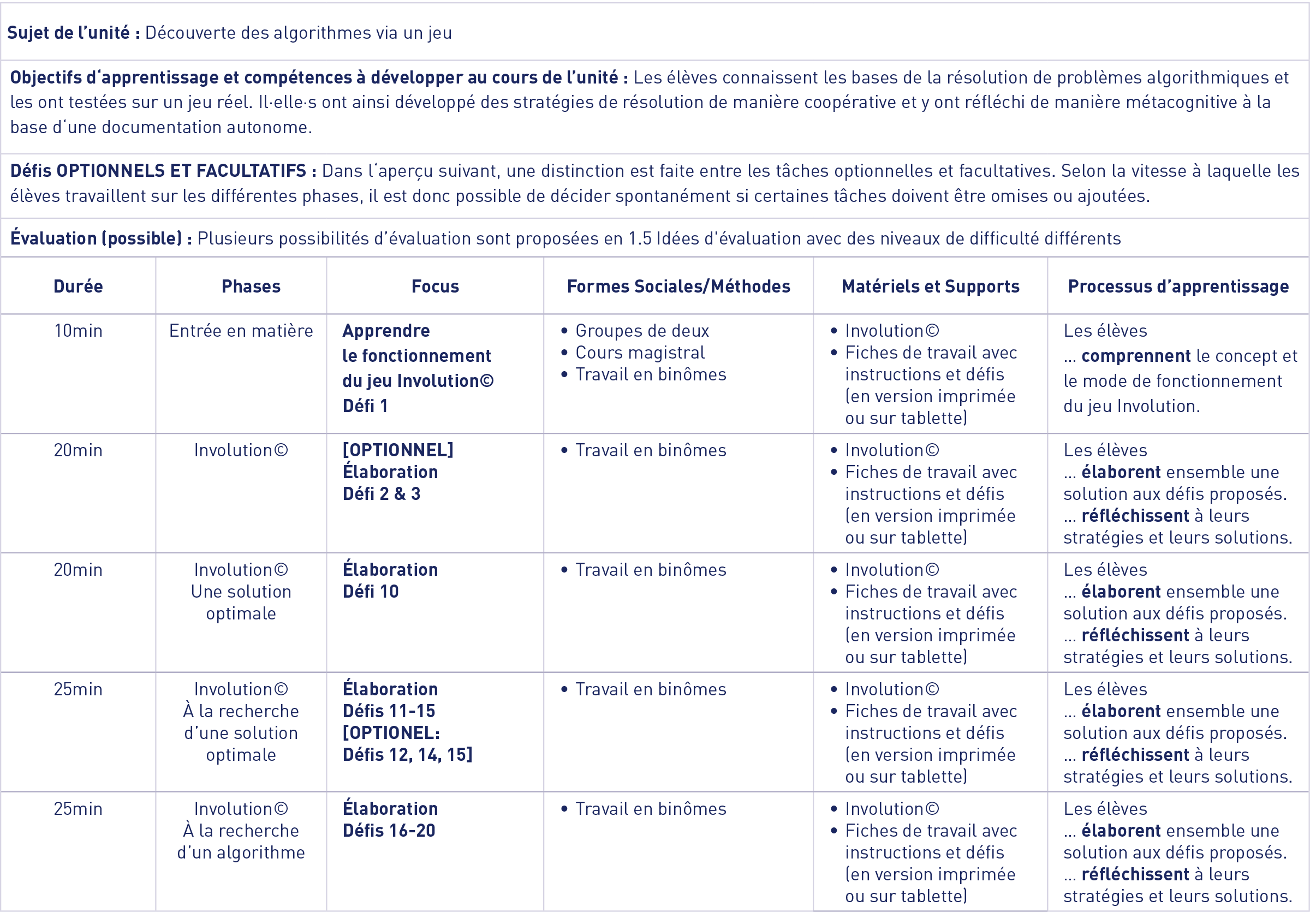
Déroulement de l’unité
Dans ce module, les élèvent jouent à un jeu baptisé Involution©. Le jeu est composé d’un plateau et d’une manivelle. Le plateau contient 10 cavités qui contiennent chacune 1 anneau noir ou blanc.

Une manivelle en forme de cercle est placée sur le jeu et par un mouvement de rotation, les anneaux changent de position. Le but du jeu est de changer la position des anneaux afin d’obtenir une configuration donnée à partir d’une configuration de départ.
Le jeu
L’enseignant·e explique rapidement le principe du jeu. L’entrée en matière se passe directement par le jeu. Les élèves se répartissent en binômes. Chaque groupe reçoit une boîte qui contient un plateau de jeu (à assembler) et des cartes de défis. Chaque carte présente deux configurations. Le défi consiste à passer de la configuration en haut à la configuration en bas de la carte en tournant la manivelle. Les élèves commencent à faire les défis dans l’ordre donné. Cette activité constitue le premier défi d’une longue liste de défis qui constituent ce module. Tous les défis sont donnés dans les matériels pédagogiques.
Après cette initiation, les élèves passent aux différents défis. Les explications ci-dessous concernent ces mêmes défis. Le module comprend de nombreux défis. Dans le meilleur des cas, tous les défis seront réalisés. Les défis munis d’une étoile sont plus compliqués (et de nature plus mathématique). Ils sont destinés aux élèves les plus motivé·e·s. En outre, d’autres défis sont optionnels (comme montré dans la planification détaillée de l’unité plus bas). Les laisser de côté n’empêche pas la réalisation du module.
Défi 2 : après une première phase, quand les élèves ont compris le principe du jeu, il·elle·s passent au défi 2. L’enseignant·e divise la classe en trois groupes ; un groupe travaille sur le premier des trois défis, l’autre sur le deuxième et le dernier sur le troisième. Le premier défi est légèrement plus simple que les deux autres : tenez-en compte lors de la division de la classe en groupes et de la répartition des défis.
Une fois le défi résolu, les élèves doivent se mettre d’accord au sein de leur groupe, puis communiquer leur résultat au reste de la classe.
Défi 3* : le défi 3, plus compliqué, est optionnel. À réaliser avec des élèves motivé·e·s et d’un bon niveau.
Comment obtenir toutes les configurations ?
Cette section aide les élèves à résoudre le défi 3. Elle concerne donc uniquement les élèves qui l’ont essayé. Parmi les défis présents dans cette section, le défi 9 est d’un niveau particulièrement élevé. Nous laissons le choix à l’enseignant·e de décider quel·le·s élèves peuvent/doivent résoudre les défis de cette section sans ou avec le défi 9.
Cette section guide les élèves vers une résolution du défi 3 via le principe mathématique de l’induction (sans pour autant en parler, ni même le mentionner).
Une solution optimale
Défi 10 : au défi 10, les élèves cherchent une solution et comptent le nombre de mouvements qu’il·elle·s font pour arriver à la solution. Il·elle·s comparent leurs solutions entre eux·elles.
En débat dirigé, il est conclu qu’une solution est meilleure qu’une autre si elle requiert moins de mouvements.
Une définition semblable à la suivante est établie ensemble en plénière :
Une solution est optimale si elle est réalisée avec le moins de mouvements possible.
À la recherche d’une solution optimale
Comment trouver cette solution optimale ? Faire le lien avec la recherche de l’itinéraire le plus court dans le métro de New York, vue en cours de Digital Sciences 1.
Comment représenter le jeu sous forme de graphe ?
Cette section commence par un exemple plus simple : le jeu Involution©, mais avec seulement 5 anneaux et un plateau de jeu réduit. Les 5 cavités les plus à droite ne doivent pas être utilisées. Il n’y a donc que 2 positions possibles pour poser la manivelle.
Défi 11 : l’enseignant·e divise la classe en trois groupes. Au sein de chaque groupe, les élèves restent en binômes pour jouer.
- Le premier groupe joue avec 1 anneau noir (et 4 anneaux blancs).
- Le deuxième groupe joue avec 2 anneaux noirs (et 3 anneaux blancs).
- Le troisième groupe joue avec 3 anneaux noirs (et 2 anneaux blancs).
Les élèves résolvent leur cas en binôme. Ensuite, il·elle·s discutent au sein de leur groupe, puis communiquent leur résultat au reste de la classe.
Défi 12* : ce défi est plus compliqué et optionnel.
Les élèves passent à la représentation graphique du jeu (à l’aide du même jeu réduit).
Défi 13 : pour ce défi et les suivants, le concept de graphe doit être introduit ou brièvement rappelé. Les élèves travaillent en binômes, puis comparent leurs résultats. Il·elle·s vont constater que le deuxième et troisième cas sont exactement les mêmes. En débat dirigé, les élèves sont amené·e·s au fait que ces deux cas sont symétriques.
Défi 14 : une fois le graphe construit, le défi 12 devient beaucoup plus simple. Les élèves vont voir la réponse clairement dans les graphes.
Lors de la phase suivante, les élèves repassent au jeu avec 10 anneaux (5 anneaux noirs et 5 anneaux blancs).
Défi 15* : ce défi est optionnel. L’idée du défi est de montrer aux élèves que les exercices de comptage deviennent compliqués à mesure que la complexité du problème augmente. Beaucoup d’élèves ne s’en rendent pas forcément compte, car compter est très simple quand il y a peu d’objets.
La représentation graphique du jeu Involution© est donnée, mais elle est trop grande pour chercher le plus court chemin à l’œil nu.
À la recherche d’un algorithme
Pour faciliter la recherche d’un algorithme, les élèves passent à 6 anneaux (3 noirs et 3 blancs). Le graphe d‘Involution© à 6 anneaux est assez petit pour chercher le plus court chemin à la main (contrairement au graphe d’Involution© à 10 anneaux), mais assez grand pour que la solution ne soit pas ridicule (contrairement à Involution© à 5 anneaux).
Défis 16 et 17 : ces défis servent à mettre les élèves sur la voie d’un algorithme. Ces défis sont résolus en binômes. Les résultats sont ensuite discutés en classe sous forme de débat dirigé.
Défi 18 : dans ce défi, l’algorithme est établi à la main. Les élèves doivent rédiger des instructions informelles. Le point b) est plus complexe. Il est destiné seulement aux élèves motivé·e·s.
Pour dessiner l’organigramme, les élèves ont le choix de le dessiner de zéro, ou d’utiliser l’aide qui leur fournit déjà les champs. Les élèves doivent ensuite mettre les champs dans le bon ordre et ajouter les flèches pour former un organigramme.
Défi 19 : ce défi ne sert qu’à montrer aux élèves que l’algorithme général est exactement le même que celui qu’il·elle·s viennent d’établir. Ce défi est à faire directement en débat dirigé.
Défi 20 : en débat dirigé, les élèves réalisent que l’algorithme qu’il·elle·s viennent d’établir est un algorithme de recherche du plus court chemin. Les mêmes types d’algorithme sont utilisés par les navigateurs GPS (voir 1.6.02. L’importance de la théorie des graphes dans les sciences numériques).
06
Possibilités de différenciation
Pour les débutants
Le module est tout à fait faisable en laissant tomber les défis et la section munis d’une étoile. Encouragez les élèves de faible niveau à faire le module sans ces défis.
Pour les plus motivé·e·s
Incluez les défis munis d’une étoile (et la section munie d’une étoile) pour les élèves plus motivé·e·s. Ces défis sont de nature un peu plus mathématique et incluent des raisonnements logiques. Il existe également un défi muni de 2 étoiles. Il est uniquement destiné aux élèves de très bon niveau qui accrochent bien au sujet.
Dans les défis 2 et 11, l’enseignant·e peut constituer les trois groupes de manière à ce que le groupe traitant le cas le plus simple soit constitué d’élèves d’un niveau plus faible.
Le défi 18, c’est-à-dire le défi principal où l’algorithme est établi, possède trois niveaux de difficulté :
- L’établissement d’un algorithme qui ne compte que le nombre minimal de mouvements et où les champs de l’organigramme sont déjà donnés.
- Idem mais sans les champs de l’organigramme.
- L’établissement d’un algorithme qui compte le nombre minimal de mouvements et la suite des mouvements.
07
Autres critères à remplir dans le cadre de la série des unités
- Contexte luxembourgeois : le jeu Involution© a été inventé par Hugo Parlier et Bruno Teheux, deux chercheurs en mathématiques de l’Université du Luxembourg. Dans sa forme actuelle, il peut être rattaché aux contenus du Guide de référence pour l’éducation aux et par les médias luxembourgeois et correspond à l’axe thématique I de Digital Sciences.
- Différenciation : plusieurs défis du module sont optionnels. Les défis marqués par une étoile sont plus compliqués que les autres et peuvent être utilisés, ou pas, selon le niveau de la classe et/ou des élèves.
- Guide de référence pour l’éducation aux et par les médias : voir les objectifs d’apprentissage visés par le guide de référence dans la section de l’analyse didactique du présent document.
- Modèle des 4 C : communication, collaboration, créativité, pensée critique :
Le modèle 4C est appliqué de diverses manières à travers les différentes formes sociales et activités d’enseignement. - Lien avec la recherche actuelle : les défis d‘Involution© font partie de la famille des problèmes de reconfiguration (Combinatorial reconfiguration), un domaine de recherche actuel qui est étudié en mathématiques et en informatique. Les algorithmes de plus court chemin ont plus de 50 ans, mais font toujours l’objet de recherches afin d’optimiser les applications de recherche de plus court chemin.
- Lien avec la recherche au Luxembourg : le jeu Involution© a été développé par deux chercheurs de l’Université du Luxembourg. Dans le podcast de la section 1.7 Parole aux scientifiques, Hugo Parlier explique comment il développe des jeux en utilisant les résultats de ses recherches.
Références
Institut national de recherche en sciences et technologies du numérique (INRIA). (2020). Éducation et Numérique : enjeux et défis. Livre Blanc N 04. https://hal.inria.fr/hal-03051329v2/document
Han, Sheon. (2022). How to Write Software With Mathematical Perfection. Quantamagazine. https://www.quantamagazine.org/computing-expert-says-programmers-need-more-math-20220517