In diesem Modul werden wir ein Spiel namens Involution© spielen. Das Spiel besteht aus einem Spielbrett und einer Kurbel. Das Spielbrett hat 10 Vertiefungen, die jeweils 1 Ring (einer bestimmten Farbe) enthalten.

Die Ringe können — wie im folgenden Video gezeigt — bewegt werden:

Challenge 1

Bildet Zweiergruppen und spielt das Spiel Involution©: Versucht, die Challenges auf den Karten zu lösen. 

Challenge 2

Ist es möglich, ausgehend von der linken Konfiguration zur rechten Konfiguration zu gelangen?

Wenn ja, erklärt eure Kurbelbewegungen. Wenn nein, warum nicht?

Challenge 3*

Kann man zu allen Ringkonfigurationen gelangen? Wenn ja, warum? Wenn nein, welche sind nicht möglich? Begründet eure Entscheidung.

Um klarer zu sehen, spielen wir das Spiel jetzt mit 9 weißen Ringen und einem schwarzen Ring.

Die entscheidende Frage ist folgende:

Challenge 4*

Ist es möglich, von einer beliebigen Konfiguration zu folgender Konfiguration zu gelangen? Begründet eure Entscheidung.

Spielen wir jetzt mit zwei schwarzen Ringen.

Challenge 5*

Ist es möglich, von einer beliebigen Konfiguration zu folgender Konfiguration zu gelangen? Verwendet eure Lösung aus Challenge 4 und begründet eure Entscheidung.

Spielen wir jetzt mit drei schwarzen Ringen.

Challenge 6*

Verwendet die Lösung aus Challenge 5, um herauszufinden, ob ihr von jeder beliebigen Konfiguration zu folgender Konfiguration

gelangen könnt.

Spielen wir jetzt mit vier schwarzen Ringen.

Challenge 7*

Verwendet die Lösung aus Challenge 6, um herauszufinden, ob ihr von jeder beliebigen Konfiguration zu folgender Konfiguration

gelangen könnt.

Challenge 8*

Schaut euch nochmal Challenge 3* an.

Challenge 9**

Und wenn wir das gleiche Spiel mit 12 Ringen spielen (6 schwarze und 6 weiße), ist es dann möglich, zu allen Konfigurationen zu gelangen? Und mit 100 Ringen (50 schwarze und 50 weiße)?

Spielen wir jetzt wieder mit 10 Ringen.

Challenge 10

Findet ausgehend von der folgenden Konfiguration

die folgende Konfiguration

und zählt die Anzahl der Kurbelbewegungen. 

Vergleicht eure Lösungen untereinander. Welche ist die beste? Legt ein Kriterium fest, nach dem beurteilt werden kann, welche Lösung besser ist als eine andere.

Vervollständigt nach der Diskussion die folgende Definition:

Eine Lösung ist optimal, wenn…

Wir werden unser Spiel nun bildhaft darstellen, um nach einer optimalen Lösung zu suchen. Erinnern wir uns daran, dass im Fach Digital Sciences 1 einer der ersten Algorithmen, mit denen wir zu tun hatten, ein Algorithmus war, um mit der New Yorker U-Bahn eine Route zu finden. So wie der U-Bahn-Plan eine grafische Darstellung des echten Streckennetzes ist, werden wir nun das Spiel grafisch darstellen: Die Knoten des U-Bahn-Netzes sind die verschiedenen Konfigurationen des Spiels (bei der U-Bahn waren die Knoten die Stationen) und zwei Konfigurationen sind durch eine Linie verbunden, wenn man mit einer Kurbelbewegung von einer Konfiguration zur anderen gelangen kann (im Fall der U-Bahn waren zwei Stationen durch eine Linie verbunden, wenn man mit der U-Bahn direkt von einer Station zur anderen fahren konnte).

Schauen wir uns das anhand eines Beispiels an. Wir spielen das Spiel Involution©, aber nur mit 5 Ringen und einem verkleinerten Spielbrett (nehmt dasselbe Spielbrett, aber ihr dürft die 5 Vertiefungen ganz rechts nicht benutzen). Daher dürft ihr nur zwei Bewegungen mit der Kurbel machen. 

Challenge 11

Die Klasse wird in 3 Gruppen geteilt. 

• Die erste Gruppe spielt mit 1 schwarzen Ring (und 4 weißen Ringen).
• Die zweite Gruppe spielt mit 2 schwarzen Ringen (und 3 weißen Ringen).
• Die dritte Gruppe spielt mit 3 schwarzen Ringen (und 2 weißen Ringen). 

Zeichnet in Zweiergruppen alle möglichen Konfigurationen eures Involution©-Spezialfalls. 

Diskutiert und überlegt gemeinsam, wie viele Konfigurationen möglich sind. Präsentiert anschließend eure Lösung und eure Erklärung vor der ganzen Klasse.

Challenge 12*

Findet heraus, ob ihr in eurem Fall zu jeder beliebigen Konfiguration gelangt, und begründet eure Entscheidung.

Wir gehen jetzt zur grafischen Darstellung über.

Challenge 13

Gebt jeder Konfiguration einen Namen (z. B. C₁, C₂, C₃ usw.). Zeichnet für jede gefundene Konfiguration aus Challenge 11 einen Knoten und notiert daneben dessen Namen. Verbindet dann zwei Knoten mit einer Linie, wenn man mit einer einzigen Kurbelbewegung von einer Konfiguration zur anderen gelangt. Vergleicht eure Graphen. 

Challenge 14

Geht zurück zu Challenge 12 (verwendet den Graphen, den ihr gerade erstellt habt). 

Wir spielen jetzt wieder mit 10 Ringen. 

Challenge 15*

Könnt ihr die Anzahl der verschiedenen Konfigurationen berechnen oder zumindest eine Obergrenze angeben?

Insgesamt gibt es 252 verschiedene Konfigurationen. Das ergibt also einen Graphen mit 252 Knoten, der wie folgt aussieht.

Der Involution©-Graph mit 10 Ringen ist viel zu groß, um den kürzesten Pfad mit bloßem Auge zu sehen. Deshalb brauchen wir einen Algorithmus.

Challenge 16

Spielt das Spiel jetzt mit 6 Ringen (3 schwarze und 3 weiße) und einem verkleinerten Spielbrett (nehmt dasselbe Spielbrett, aber ihr dürft die 4 Vertiefungen ganz rechts nicht benutzen). Findet alle möglichen Konfigurationen und zeichnet den Graphen. 

Challenge 17

Verwendet den in Challenge 16 gefundenen Graphen, um zu bestimmen, was eine optimale Lösung ist, um zu der folgenden Konfiguration zu gelangen

ausgehend von folgender Konfiguration:

Challenge 18

Lasst euch von der letzten Challenge inspirieren und sucht einen Algorithmus für 

1. die geringstmögliche Anzahl an Kurbelbewegungen, um von einer Konfiguration zur anderen zu gelangen (sobald der Graph des Spiels erstellt wurde),
   
   Hilfe
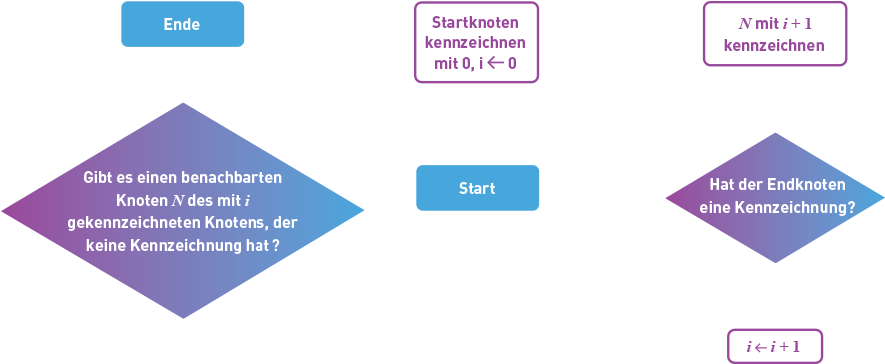
2. eine optimale Lösung, um von einer Konfiguration zur anderen zu gelangen (sobald der Graph des Spiels erstellt wurde).
   
   Hilfe

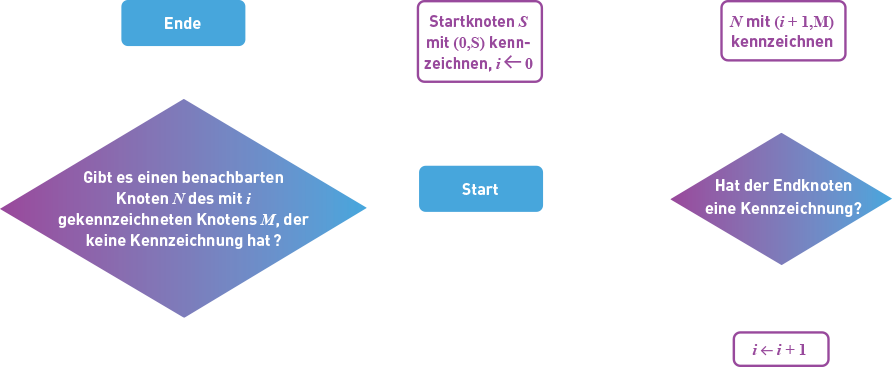
Schreibt die informellen Anweisungen für euren Algorithmus auf und zeichnet ein Flussdiagramm.

Challenge 19

Verallgemeinert den Algorithmus im Spiel Involution© mit 10 Ringen. 

Challenge 20

Schaut euch das folgende Bild an:

Um welche Anwendung handelt es sich? 

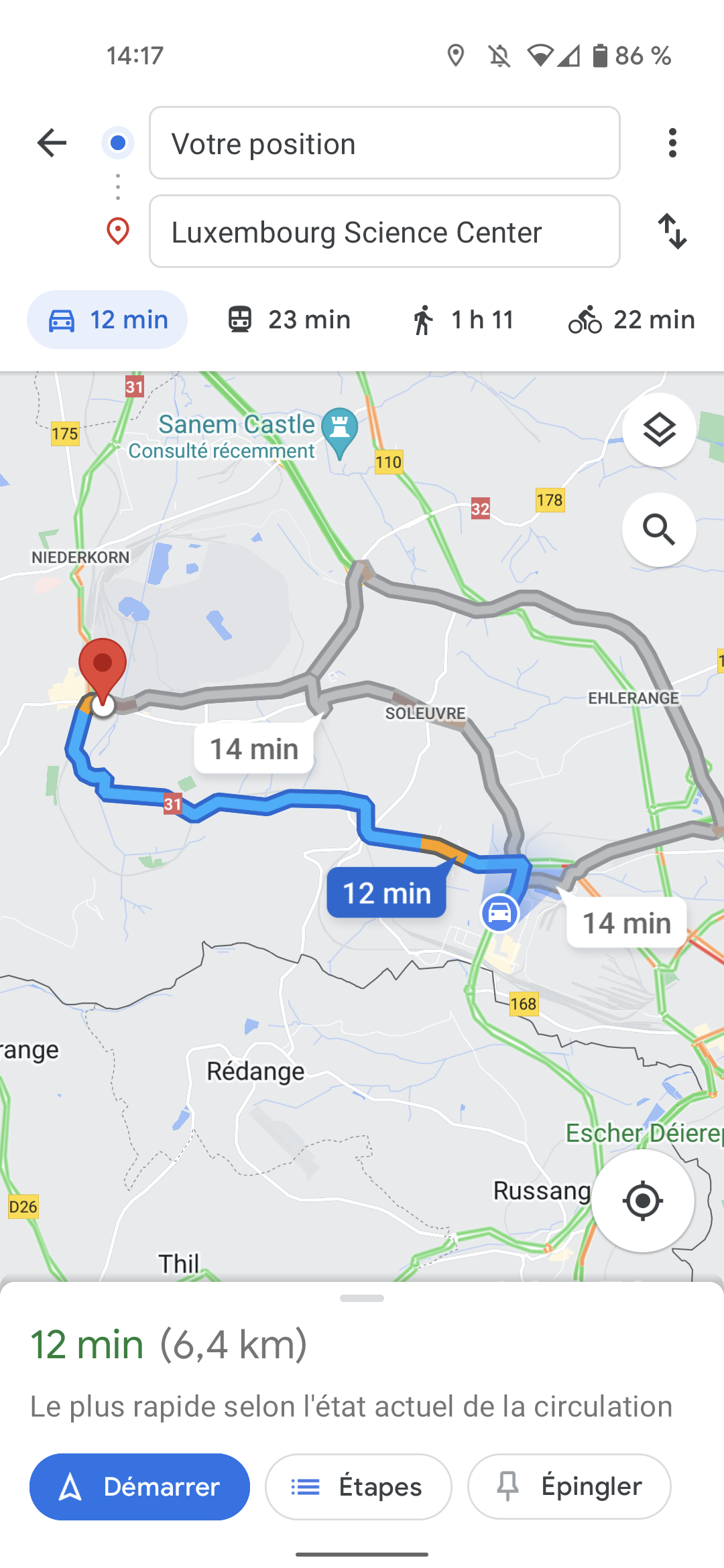
Sucht eine Verbindung zwischen dieser Anwendung und der Suche nach einer optimalen Lösung im Spiel Involution©.