Attention : À la fin de ce module, l'utilité de la somme pondérée est démontrée en illustrant qu'elle permet de détecter les erreurs d'inversion de deux chiffres consécutifs. Le fait que cela ne soit possible que lorsque la différence entre les deux chiffres n'est pas égale à 5 est omis pour ne pas compliquer davantage le raisonnement.
2.5 Pour aller plus loin
01
Les origines des codes-barres
Les codes-barres ont été inventés aux États-Unis sous le nom de UPC : Universal Product Code. Dans la vidéo suivante le chroniqueur et humoriste David Castello-Lopes raconte l’histoire des codes-barres et comment le premier code-barres a été scanné le 26 juin 1974.
Malgré leur nom, les codes-barres UPC n’étaient pas du tout universels. Leur utilisation n’était possible qu’aux États-Unis. C’est pourquoi en Europe, en 1977, on a inventé un nouveau système de codes-barres appelé EAN : European Article Number. Cependant, au lieu d’inventer un système concurrent avec le système américain, le EAN étend le UPC américain de manière ingénieuse. Le système UPC contient 12 chiffres, alors que le système EAN en contient 13, mais de telle manière qu’un code-barres EAN commençant par 0 équivaut à un code-barres UPC sans le premier 0. Ainsi, les Américains ont pu continuer à utiliser leur système pendant que le reste du monde utilisait des codes-barres EAN ne commençant pas par 0. Depuis 2005, les Américains ont aussi adopté la version européenne du code-barres mais en l’appelant UPC-13 (Jones, 2009).
02
Le fonctionnement des codes-barres
Dans le reste du texte nous allons nous restreindre aux codes-barres EAN à 13 chiffres. Cette partie est majoritairement basée sur (Stammbach, 2006).
Un numéro EAN se décompose en 4 blocs dont les significations respectives sont détaillées ci-dessous (les livres et revues constituent un cas particulier qui sera examiné plus loin). Les deux premiers chiffres correspondent au pays producteur (Made in…). Les dix chiffres suivants identifient l’entreprise productrice et le numéro de l’article au sein de cette entreprise.
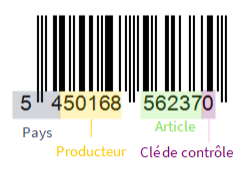
Le tableau suivant montre les codes de quelques pays (IREM, 2000).
| États-Unis, Canada | 00-09 |
| France | 30-37 |
| Allemagne | 40-43 |
| Japon | 49 |
| Grande-Bretagne | 50 |
| Belgique | 54 |
| Danemark | 57 |
| Italie | 80-81 |
| Suisse | 76 |
| Autriche | 90-91 |
| Pays-Bas | 87 |
Le code-barres du yaourt LUXLAIT, également utilisé dans le module, montre que le Luxembourg utilise le même code que la Belgique, probablement en raison de l’union économique entre ces deux pays.
Comme vu dans ce module, le 13e chiffre est une clé de contrôle. L’algorithme veut que si ( a_1a_2a_3a_4a_5a_6a_7a_8a_9a_{10}a_{11}a_{12}a_{13} ) est le code-barres, alors (a_{13} ) vaut 10 moins le reste de la division euclidienne de
\[ a_1+3a_2+a_3+3a_4+a_5+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12} \]
par 10.
Autrement dit
\[ a_1+3a_2+a_3+3a_4+a_5+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12} \]
est un multiple de 10. Ceci peut aussi être exprimé en termes de calcul modulaire :
\[ a_{13} equiv -(a_1+3a_2+a_3+3a_4+a_5+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12}) pmod {10} \]Cette clé de contrôle sert en premier lieu à identifier les fautes de lecture. Le lecteur de code-barres lit le code-barres et vérifie qu’il s’agit bien d’un code-barres correct à l’aide de l’algorithme. Si c’est le cas, il émet un bip et transmet l’article et le prix à la caisse. Si la clé de contrôle n’obéit pas à l’algorithme, le lecteur n’admet pas le code-barres. Il a identifié la faute de lecture et il faut rescanner l’article.
Proposition : Les codes-barres ne permettent pas seulement au scanner d’identifier une faute de lecture, mais aussi de scanner un article même si un des chiffres est illisible.
Preuve : Supposons d’abord qu’un des chiffres de rang impair soit illisible. Sans perte de généralité, supposons que (a_5) est illisible. Reprenons l’équation modulaire, et nous obtenons :
\[ a_{5} equiv -(a_1+3a_2+a_3+3a_4+3a_6+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12}+a_{13}) pmod {10} \]Comme (a_5 ) est un chiffre (donc ( 0 leq a_5 leq 9) il y a une solution unique à cette équation modulaire.
Supposons maintenant qu’un des chiffres de rang pair soit illisible, et sans perte de généralité, supposons que (a_6) soit illisible. Alors nous avons :
\[ 3a_{6} equiv -(a_1+3a_2+a_3+3a_4+a_5+a_7+3a_8+a_9+3a_{10}+a_{11}+3a_{12}+a_{13}) pmod {10} \]Comme 3 et 10 sont premiers entre eux, 3 a un inverse modulo 10. En fait le produit de 3 et 7 vaut 1 modulo 10. En multipliant les deux côtés de l’équation par 7, nous obtiendrons une valeur pour (a_6 ) qui sera unique car (a_6 ) est un chiffre.
Un lecteur attentif notera que la démonstration précédente demeure inchangée sans la somme pondérée. Alors, quelle est l’utilité de cette somme pondérée ? En effet, elle sert à détecter une erreur humaine qui intervient quand le caissier ou la caissière doit taper le code-barres à la main : l’inversion de deux chiffres consécutifs.
Proposition : L’algorithme du code-barres EAN détecte l’inversion de deux chiffres consécutifs sauf si leur différence vaut 5.
Preuve : Soit ( a_1a_2a_3a_4a_5a_6a_7a_8a_9a_{10}a_{11}a_{12}a_{13} ) un code-barres et inversons (a_i ) et (a_{i+1} ). Si les deux codes-barres sont des codes-barres valides, nous avons :
\[ begin{align} a_{13} & equiv & -(a_1+3a_2+…+a_i+3a_{i+1}+…+3a_{12}) pmod {10} \ a_{13} & equiv & -(a_1+3a_2+…+a_{i+1}+3a_i+…+3a_{12}) pmod {10} end{align} \]Nous avons donc :
\[ a_1+3a_2+ ldots +a_i+3a_{i+1}+ ldots +3a_{12}) equiv a_1+3a_2+ ldots +a_{i+1}+3a_i+ ldots +3a_{12} pmod {10}. \]Cette dernière équation est vérifiée si et seulement si la différence (a_i-a_{i+1} ) est un multiple de 5. Comme (a_i) et (a_{i+1} ) sont des chiffres, la différence est un multiple de 5 si et seulement si (a_i = a_{i+1}) ou ( vert a_i – a_{i+1} vert = 5).
L’inversion de deux chiffres de rang pair ou de deux chiffres de rang impair ne sera malheureusement pas détectée par l’algorithme du code-barres.
Une mesure de sécurité comme la clé de contrôle permet donc d’éviter une partie des erreurs, mais pas toutes. C’est toujours le cas. Le système est bon lorsqu’il réduit significativement la fréquence des erreurs dans leur ensemble. Il est d’autant plus effectif plus la réduction de la capacité d’erreur globale est importante. Pour pouvoir juger de ce dernier point, il faut connaître la prévalence des différents types d’erreurs. Une étude basée sur la langue anglaise a permis de constater la prévalence des erreurs lors de la transmission de suites de chiffres (oralement ou par saisie) (Stammbach, 2006) :
- Les faux chiffres constituent 79,1% des fautes.
- L’inversion de deux chiffres consécutifs constitue 10,2 % des fautes.
- Tous les autres types d’erreurs sont inférieurs à 1 %.
Aujourd’hui, les codes-barres ne sont pas seulement utilisés pour désigner des produits, mais ils sont également utilisés – de manière modifiée – à de nombreuses autres fins. La raison en est la large diffusion du système initial. Cela a eu pour conséquence que les lecteurs ont pu être fabriqués en très grand nombre et donc à bon marché. Ainsi nous les trouvons aussi sur toutes nos cartes de fidélité, carte de bibliothèque ou même sur notre carte de CNS.

03
Le code ISBN
Lorsqu’on examine un livre récent, on constate qu’il est muni d’un code-barres, tout comme les produits de supermarché. En revanche, un livre plus ancien, publié avant 2007, possède à la fois un code-barres EAN et un numéro ISBN à 10 éléments.

L’abréviation ISBN signifie International Standard Book Number. Le système ISBN repose sur un principe similaire à celui de l’EAN, mais avec une touche d’ingéniosité supplémentaire. Les 10 éléments du code ISBN prennent les valeurs de 0 à 9 et X qui représente le nombre 10 (merci aux mathématiciens Romains). Les neuf premiers éléments (a_1 ) à ( a_9 ) déterminent le livre de manière univoque et le dixième élément (a_{10} ) est une clé de contrôle qui est obtenue de la manière suivante
\[a_{10} equiv -(10a_1 + 9a_2 + 8a_3+7a_4+6a_5+5a_6+4a_7+3a_8 + 2a_9 ) pmod {11} \]Tout comme le code EAN, le code ISBN détecte les erreurs de lecture et permet de reconstituer un chiffre illisible (les preuves étant très similaires).
Cependant, contrairement au code EAN, l’ISBN permet toujours de détecter l’inversion de n’importe quels deux éléments.
Preuve : Imaginons que les éléments (a_i ) et (a_k ) ont été inversés pour ( 1 leq k leq 9 ). Alors
\[ begin{align}a_{10} equiv -(10a_1 + 9a_2 + … +(11-i)a_i + …. + (11-k)a_k + … + 2a_9 ) pmod {11} \
a_{10} equiv -(10a_1 + 9a_2 + … +(11-i)a_k + … + (11-k)a_i + … + 2a_9 ) pmod {11}
end{align}
\]
Ces deux équations sont équivalentes à
\[ (a_i-a_k)(k-i) equiv 0 pmod 11. \]Comme ( 0 leq vert k – i vert leq 9 ) et tous les nombres entre 1 et 9 sont premiers à 11 (car 11 est un nombre premier), nous avons
\[ a_i-a_k equiv 0 pmod 11. \]Les éléments (a_i ) et (a_k ) prennent des valeurs de 0 à 10, ce qui entraîne que (0 leq vert a_i – a_k vert leq 10 ). La seule solution à l’équation précédente est donc que (a_i = a_k ).
Malgré la performance du code ISBN, le numéro ISBN est passé de 10 à 13 chiffres en 2007 (Stammbach, 2006).
04
Les comptes IBAN
Actuellement en Europe, nous utilisons des numéros de compte IBAN (International Bank Account Number), un système international de numérotation des comptes bancaires. Un IBAN est composé d’au plus 34 caractères, dont :
- Les deux premiers caractères indiquent le code du pays (par exemple, LU pour le Luxembourg, BE pour la Belgique, DE pour l’Allemagne, FR pour la France, etc.),
- Les deux caractères suivants constituent la clé de contrôle,
- Les au plus 30 derniers caractères représentent le numéro de compte.
L’IBAN facilite ainsi les virements et prélèvements de compte à compte, que ce soit au sein d’un même pays ou lors d’opérations sur des comptes détenus dans des banques de différents pays.
Contrairement aux exemples vus précédemment, l’IBAN comporte deux chiffres pour la clé de contrôle. Celle-ci ne se situe pas à la fin mais en troisième et quatrième position. L’algorithme utilisé pour obtenir cette clé de contrôle diffère des précédents mais reste assez similaire (Mathelounge, 2019) :
- On considère le code IBAN et on enlève les deux lettres du début ainsi que les deux chiffres de la clé de contrôle.
- Les lettres sont transformées en nombres en utilisant le système A=10, B=11, C=12, … (autrement dit, chaque lettre est remplacée par le nombre qui la représente en ASCII moins 55).
- Le nombre constitué de 4 chiffres formés par les deux lettres est ajouté à la fin du numéro de compte restant. Ainsi on obtient un nombre d’au plus 34 chiffres.
- On calcule le reste de la division du nombre de l’étape 4 par 97.
- Les deux chiffres de la clé de contrôle forment le résultat de 98 moins le reste obtenu à l’étape 5.
Ainsi, un système de ebanking peut vérifier si le numéro de compte indiqué sur un virement est effectivement un numéro de compte IBAN valide. Si ce n’est pas le cas, le virement est refusé.
Comme 97 est un nombre premier, ce système permet aussi de retrouver le numéro IBAN quand un chiffre est illisible.
Ceci me rappelle une histoire que j’ai vécue lors du mariage d’une amie mathématicienne. En guise de cadeau, ses amis avaient rassemblé une somme d’argent pour le couple, mais ils avaient prévu une série d’épreuves amusantes avant de leur remettre le précieux butin.
Après avoir brillamment réussi les épreuves, les amis, avec une solennité théâtrale, annoncèrent qu’ils avaient déposé l’argent sur un compte bancaire. Pour y accéder, le couple devait utiliser leur carte d’identité et le numéro IBAN du compte. Ils leur remirent alors une feuille avec le numéro IBAN… mais il manquait un chiffre !
Avec un sourire malicieux, les amis présentèrent un bol rempli de confettis colorés, en déclarant que le chiffre manquant se trouvait sur l’un des confettis. Mon amie, gémissant au grand plaisir des invités, se mit à chercher le confetti sans aucune chance de réussite. Son mari et elle abandonnèrent disant qu’ils allaient chercher plus soigneusement à la maison.
Plus tard dans la soirée, elle vint chez moi, un sourire complice aux lèvres. Je lui fis un clin d’œil et lui dis qu’il ne fallait absolument pas chercher dans ce bol de confettis. Elle me confia alors, en riant, qu’elle le savait, mais qu’elle ne voulait pas gâcher la surprise pour ses amis.
C’est donc grâce aux mathématiques qu’un couple fraîchement marié peut gagner de l’argent sans se perdre la tête dans des confettis.
05
Le QR code
Les codes-barres sont progressivement remplacés par leurs homologues bidimensionnels : les QR codes. QR signifie Quick Response. Inventés en 1994 par la société japonaise DENSO Corporation pour améliorer la traçabilité des pièces dans les usines Toyota, les QR codes se distinguent par leur rapidité de lecture et leur résistance aux dommages, comme les taches d’huile. Aujourd’hui, les QR codes sont omniprésents : des publicités aux pages web, en passant par les cartes de visite.
Toutefois, comme d’autres moyens physiques de stockage de données, les QR codes sont sujets à des erreurs. Pour garantir que les lecteurs de QR codes peuvent néanmoins traiter les informations de manière fiable lorsque des erreurs se produisent, les QR codes ne possèdent pas une, ni deux clés de contrôle, mais reposent sur un algorithme mathématique plus compliqué, appelé code de Reed-Solomon. Le principe sous-jacent est basé sur des polynômes sur des corps finis. Pour plus d’informations sur les QR codes nous vous invitions à consulter l’article très instructif de Down, Sigmon et Klima (2021). Derek Muller de la chaîne Youtube Veritatium a réalisé une vidéo explicative sur les QR codes. Il y construit un QR code en partant de zéro et explique la technologie et les mathématiques derrière cette invention. Au début de la vidéo, il raconte également de façon charmante l’histoire des codes-barres.
Références
1. Downs, Adam S., Sigmon, Neil P. and Klima, Richard E. (2021). The Mathematics of QR Codes. Asian Technology Conference in Mathematics https://atcm.mathandtech.org/EP2021/invited/21891.pdf
2. Groupe Lycée, Irem de STRSABOURG. (2000). Clés de contrôle. Repères IREM. 41.
3. Jones, Chris. (2009). How Barcodes Crossed the Atlantic. Mathematics in school 38.5 : 30–31.
4. Mathelounge. (2019). Wissensartikel: Der IBAN-Algorithmus. https://www.mathelounge.de/673376/wissensartikel-der-iban-algorithmus
5. Stammbach, Urs. (2006). EAN, ISBN, CD, DVD: Von Prüfziffern zu fehlerkorrigierenden Codes. Schweizerischer Tag über Mathematik und Unterricht. ETH Zurich.

