2.2 Lesson planning
Contents
- Euclidean division
- Equations
The student is able to
- solve problems using Euclidean division.
- use a calculator or software to perform Euclidean division and interpret the result.
- check whether a given value is a solution to an equation.
- solve a 1st degree equation of the form \[ ax + b = cx + d \].
- solve problems using a 1st degree equation.
Before the lesson
he teacher installs a barcode reader on the class tablets or asks the students to install a barcode reader on their phones. A reader that works well is for example this one:
Cognex Barcode Scanners App : Appstore or Playstore
It will be useful at the start of the lesson.
For homework, the teacher asks the students to look for barcodes on products at home and upload them to a platform (M1).
The lesson
The lesson contains many activities for the students. Not all the activities are necessary for the continuity of the lesson, and some require more effort than others. Leaving out or adding these activities is a good way of differentiating. Optional activities are indicated with a star.
There is a lot of text at the beginning of each activity and between the different exercises. We have chosen this format to allow students to work very independently and to progress at their own pace, without having to wait for explanations from the teacher. Of course, the teacher is free to change this format and give explanations at the beginning of the activity. In this case, the students can ignore the text.
These written explanations are particularly useful if the teacher has students work on optional activities. In this way, the pupils can carry on with their work without the need for additional explanations.
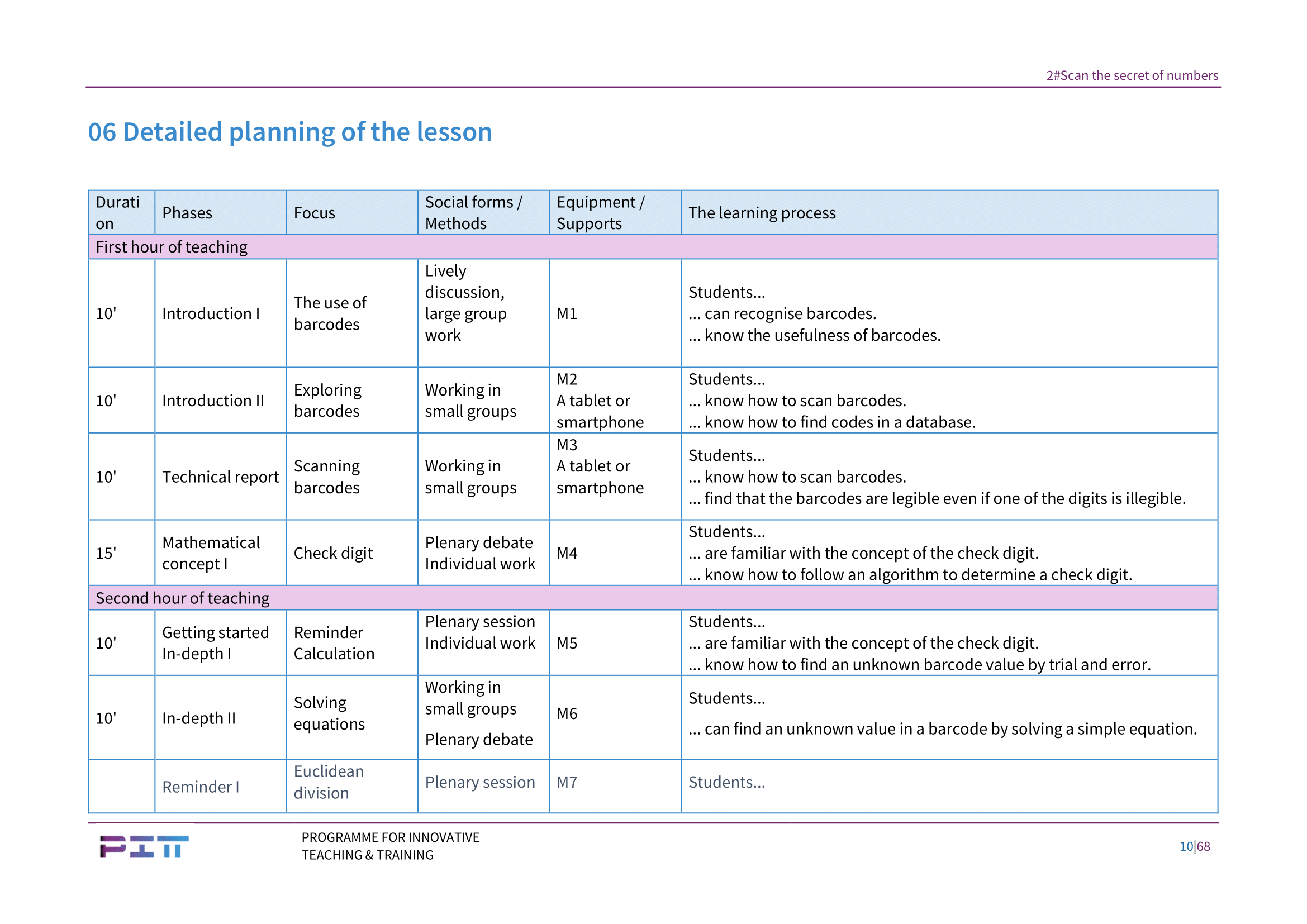
First hour of teaching
Introduction I (10 min). In plenary, the pupils discuss the barcodes they have discovered. They try to answer the question of the usefulness of barcodes (M1).
Introduction II (10 min). To understand the principle of barcodes, in groups of two or three, depending on the number of barcode scanners available, the students scan the items shown in the exercise, look for the code in the database and calculate the price (M2). No further explanation is needed. The teacher goes through the rows and checks that the two short reflections have been done.
Technical observation (10 min). The students are given lots of damaged barcodes (M3), but each is damaged in a different way. In the same groups as before, they have to try to scan the codes and see if it’s possible or not. They also have to describe the damage for each code. This exercise works best if they hide all the barcodes and leave only one visible, otherwise the reader might scan the wrong one. The teacher lets the group think about the conclusion to be drawn. Their results are then discussed in plenary. The correct conclusion to draw is that a barcode with a single illegible digit is still legible by the reader. However, if 2 or more digits are illegible, the reader will no longer be able to decipher the code. More details can be found in the Solutions section.
Introduction of the first mathematical concept (15 min). In the previous activity, the students discovered that barcodes can still be deciphered even if one of the digits is illegible. In this activity (M4), they will discover the reason behind this phenomenon: the check digit. Before starting the activity and reading the explanation, the teacher will discuss this phenomenon in plenary, which may seem magical at first: how is the barcode reader able to read a code if one of the digits is illegible? The pupils will come up with all sorts of hypotheses. The teacher does not simply dismiss the ideas, but explains why they are not valid. Then the teacher tries to put the pupils on the right track: one of the 13 digits must depend on the others (otherwise it’s impossible to guess). But how? The aim is for the pupils to work out for themselves the idea that one of the 13 digits is obtained from the others by mathematical calculation.
The next question is, of course, which mathematical calculation gives us the 13th digit. In this activity, two calculations are proposed, to show that one is better than the other. The activity consists of two exercises: the first shows that both calculations are feasible and provide a check digit. The second shows that in both cases, an error in the barcode is detected by the check digit. At the end of activity M4, the students are familiar with the concept of a check digit, but are still unaware that some calculations are more effective than others in establishing check digits. This concludes the first hour of teaching.
Second hour of teaching
Introduction (1 min). The concept of a check digit is briefly explained, as are the two methods of calculating a check digit (M5).
Exploring the first mathematical concept I (9 min). In this activity, a damaged code is given: \[ 23×2 \]. Individually, the students try to find the value of \[ x \] for this code to work, i.e. for 2 to be the check digit. They have to do this once using Alice’s method and once using Bob’s method. The value of \[ x \]
is not found by solving an equation but by trial and error, trying all possible values from 0 to 9 (M5). The results, i.e. seeing that there is only one possibility for the value of \[ x \] in the case of Alice’s code, but several possible values in the case of Bob’s code, are discussed in plenary.
Exploring the first mathematical concept II (10 min). In groups (the same groups as in the previous lesson, if possible), the pupils find the missing numbers in M6.
Note: there’s nothing complicated about this, but it does require a lot of mental calculation, which in our experience always takes longer than expected.
The conclusion (end of activity M6) is first discussed in the group, then in plenary.
***Reminder I. This activity (M7) is optional. If the teacher feels that the students need a reminder about Euclidean division, we advise them to do so.
Reminder II (10 min). Unlike the previous reminder, which was theoretical, this reminder (M8) forces the pupils to get their hands dirty and calculate the remainders of Euclidean divisions. To save time, and if the pupils are familiar with the concept of Euclidean division, the teacher might consider omitting this reminder as well. We also advise everyone to get the pupils to work in groups, with one pupil dealing with the case d=2, another with the case d=3 and another with the case d=5. We also advise everyone to do the case d=10. This will be useful later. The teacher checks that all the pupils have understood the trick for calculating the remainder of Euclidean division by 10. The second activity in this reminder (M9) deals with a property that is important for the rest of the lesson. We therefore advise you not to skip it.
***To go further. Activity M10 is out of context and goes further. It can be left out without any problem. The idea is to look at modular congruence, which is, by definition, based on the remainders of Euclidean divisions by a number. We recommend leaving it to the strongest students. They can do it in class if they are progressing faster than the others, or for homework. Modular congruence is a concept from more abstract mathematics that can arouse the interest of strong students in abstract mathematics.
Further study (13 min). This activity (M11) looks at the following property:
The sum of the remainders of the Euclidean divisions of a by d and b by d is equal to the remainder of the Euclidean division of a+b by d.
Even if some students are familiar with this property, we recommend doing this activity, as it will be important for the reasoning that follows. This activity is done partly on the Mathigon platform (follow the link indicated in M11) and partly on paper. We recommend that you let the students work in groups. To save time, some of the students can follow Alice’s approach and others Bob’s approach. Then they can put their results together and compare.
Closure (2 min). In plenary, the previous property is discussed to make sure that all the pupils have understood.
Third hour of teaching
*** Excursion into combinatorics. This part (M12) is again optional. It is not directly linked to the module, so leaving it out has no impact on the rest. However, when it comes to creating barcodes, a natural question that arises is the number of possible barcodes. That’s why we’ve included this activity, which provides a first introduction to combinatorics for the most motivated students.
Introduction of the second mathematical concept (20 min). The aim of this activity (M13) is to understand which divisor to choose in order to construct an efficient key based on the remainder of a Euclidean division. First, the basic assumptions are clearly explained in plenary (5 min):
- 3-digit code.
- The first two digits can be chosen from 0 to 6.
- Definition of the check digit.
Note: At the very beginning, there is a short combinatorial section. This can be done by some of the students (for example, those who have done the previous optional activity), ignored without affecting the rest of the module, or done by all the students.
The teacher divides the class into 9 groups, each working on one of the 9 examples in M13 for 10 minutes. The teacher makes sure that each group completes the conclusion of its example correctly. The teacher then reassembles the groups by placing one student from each example in each new group. In these new groups, the students share their conclusions and together complete the final summary table for M13 (5 min).
Conclusion (20 min). The pupils work in groups of two or three for this activity. They take the time to read the text carefully and fill in the blanks (M14). We recommend allowing enough time for this task, as the text can be complex for students to understand.
Pooling of results (5 min). In plenary, the findings from the conclusion are discussed. The teacher checks that all the students have understood why it is important to choose a divisor d > 6.
Fourth hour of teaching
Review and brainstorming (10 min). In this first part (M15), the students are asked to reflect on all the knowledge they have acquired so far in the module. They are then asked to consider how to design an effective 12-digit barcode, with an additional check digit. This serves as a transition to the second part of the lesson, where the official EAN-13 barcode is introduced.
Real-life example (30 min). First the EAN-13 barcode is presented (M16) and the instructions for calculating the check digit are explained. The teacher goes through this in plenary with the pupils (5 min). Then the pupils repeat the calculation of the check digit on two examples (the barcode of a LUXLAIT yoghurt and a barcode they find) (10 min). This activity and those that follow can be done in groups. This activity serves to reinforce the understanding of the calculation and to ensure that the students understand it. Once the calculation algorithm has been understood, we move on to error detection (M17). The students are shown three barcodes and have to decide whether or not they are correct (7 min). If the teacher realises that mental arithmetic is slowing the pupils down, he can suggest that they do this exercise in groups of 3, with each pupil working on an example. Finally, two barcodes, each with a missing digit, are presented to the pupils (M18), who have to find the missing digit (8 min).
Note 1: If the equations have already been covered in class, it is advisable to ask the pupils to find the missing digit using a correctly formulated equation. Alternatively, you can allow the pupils to find the answer by trial and error. This method may also be more appropriate for a class with mathematical difficulties.
Note 2: To make this exercise more fun, the teacher can buy products that the pupils like (fizzy drinks, sweets, etc.) and hide one of the digits in the barcode (by blackening it, for example). It is advisable to take a photo of the barcode before masking a digit. It is also advisable to repeat the exercise twice with two different products, once masking an odd-numbered digit and once masking an even-numbered digit (the solving equation varies slightly depending on the rank of the masked digit). This game can be played competitively (the first group to find the missing digit receives the product as a prize) or non-competitively (the teacher buys enough products for all the pupils, and each group gets its prize once the correct answer has been found). The final choice depends on the mood of the class and the attitude of the pupils.
***To go further. Up to this point, the module has clearly explained and demonstrated, using concrete examples, the ideas behind the EAN-13 barcode (why the digits 0 to 9, why a check digit, why the sum in the algorithm that determines the check digit, why Euclidean division by 10). What remains to be clarified is the weighted sum: why are even-numbered digits multiplied by 3? This question is addressed and resolved in activity M19. Even though this part has been left out, we advise the teacher to read it in case a student asks this question.
Closing (5 min). To close the module, the teacher leads a plenary discussion with the whole class during which he repeats the EAN-13 barcode algorithm and explains the different parts of this algorithm in relation to what has been seen during the session.
The module is designed to enable students to work independently. At the start of each section, explanations are provided so that students can begin the section without the teacher’s help. In this way, the teacher can work with the weaker students and leave the stronger, more motivated students to progress at their own pace.
For a class with mathematical difficulties, the teacher can also leave out part or all of the mathematical reasoning section (M4-M16) and concentrate on calculating the check digit in the case of EAN-13 barcodes.
- Luxembourg context: Barcodes are universal and not directly linked to Luxembourg. However, the theme is about to make the link with research carried out in Luxembourg. Part of the Mathematics Department in Luxembourg is involved in research into number theory, a field closely linked to the theory of codes and cryptography. Research into cryptography and security is also carried out by the University of Luxembourg’s Department of Computer Science and the SnT (Interdisciplinary Centre for Security, Reliability and Trust).
- Differentiation: As described in the previous paragraph, the module contains several levels of differentiation.
- Media Compass: Competences targeted by the Media Compass1:
- Competence 2 – Communication and collaboration: 2.1 Working with others
- Competence 5 – Digital world: 5.1 Resolving simple technical problems
- 4C model: communication, collaboration, creativity, critical thinking: The 4Cs are integrated into this module. During the four hours of instruction, students are asked to communicate and collaborate to solve problems. In each grouping, students’ critical thinking is stimulated in order to translate the mathematical concepts previously discussed into rules for creating a barcode. Students’ creativity is challenged early in the module when they are asked to think about how a barcode reader can decipher a damaged barcode.
4 https://edumedia.lu/wp-content/uploads/2024/12/Medienkompass_EN_web.pdf